Chess Tournament (an analysis and a story)
This article is, at the same time, a story and an analysis of a real chess tournament. However, although every game, every play and every result, are real, the short story told is fictitious.
The full analysis in R, along with data sets, is published on github following this link.
Opening
He looked at the ceiling of his room for the last time before getting up. He had not slept, at least so it seemed, his brain kept reviewing openings, tactics, pawn structures, ambushes and all kind of endings.
He must have slept more than he thought, at least he did not feel tired ... Or maybe, just was nerves.
During the last hour, when the light began to filter through the curtains, he had added an imagined board on the ceiling to his mental game, on which the pieces moved at his will.
Today was the first time he will compete in an official tournament, and his hands were sweating.
Some data
For the analysis of the tournament I had a file with all games played. From this file I deleted those games with errors for different reasons. For example:
- Not disputed because of the absence of any of the opponents.
- Error movements, either because the number of moves did not match the number in the file, either by missing plys in the PGN.
After debugging information, I eliminated personal data, the name and location of the tournament, and the names of the players, keeping the distinction of each player during the anonymization.
The resulting dataframe contains 562 items, which are those that I used in the analysis.
The sports pavilion where the tournament were to be played was prepared for the occasion. There were tables in long rows and each of them had a board and a clock. This reminded him the rules that he had just learned “you loose when you consume the allotted time”. One of his strongest concerns was running out of time. Even if it meant ending a game without receiving checkmate.
You could say that the atmosphere in the hall was very similar to a temple. He greeted several acquaintances, but did not want to engage in conversation, those were the moments before the fight and they required concentration.
He looked at the panel where was his table: with black pieces against an elo 1600. He'll try not to fall in the opening traps, try to close the position, wait his oportunity, and let the opponent to do the hard work.
This is some general information about the tournament. 165 players, with the following victories in each case:
| white | draw | black | unknown |
|---|---|---|---|
| 260 | 76 | 225 | 1 |
There is a game that has no known result in the file ( '*' in pgn notation) so I had not considered it for the analysis.
The distribution of the number of movements of games was as follows:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | NA’s |
|---|---|---|---|---|---|---|
| 1 | 56 | 72 | 76.84 | 94 | 173 | 59 |
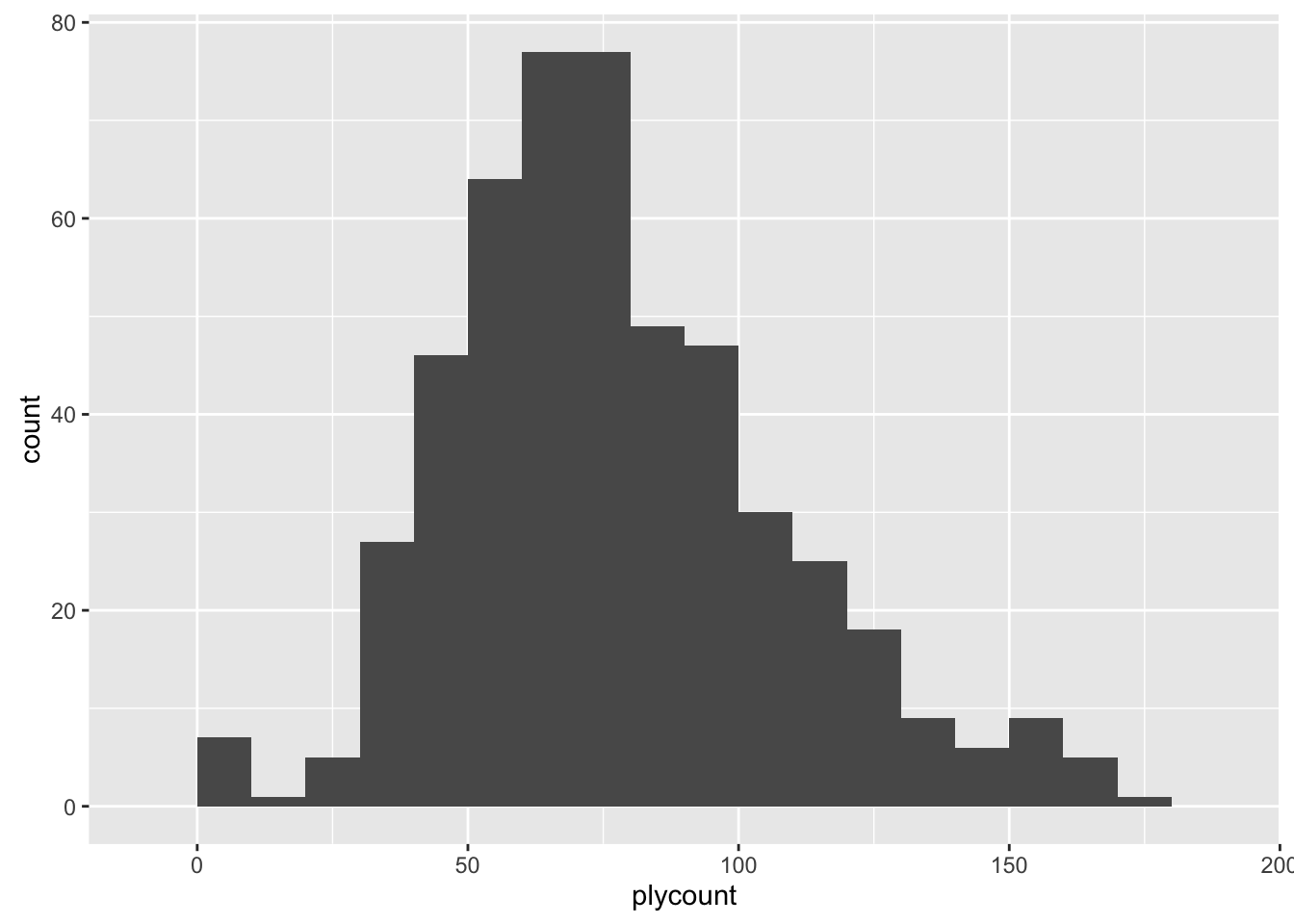
In this tournament, every game lasted on average about 77 movements, however, there are games that tooked much more. It can be seen that the histogram has a left bias, third quartile is 94 movements. Only 25% of the games tooked over 94 moves.
The histogram has a peak to the left. It corresponds to 7 games with just the first move, apparently they are those in which the opponent did not show up.
He sat in his place early, his opponent had not yet arrived. He looked around, a sea of boards and people about to start a bloodless battle. He placed his sheet at his right side, equidistant from both edges of the table, and the pen perpendicular two centimeters apart. Other players, already seated, unfurled, in turn, their quirks and tics
The first move of white player was e4, “perfect”, he thought, and answered quickly with c6. His opponent went on, without thinking, with d4, to which he responded with d5. They continued at this pace for a few more moves, including an exchange of pawns, until he was forced to think. His rival, who continued to respond quickly, had made a movement unknown to him, would it be a trap? A fail? Or it was the best move against the Caro-Kahn defense? After a good time of thinking, he responded trying to hide his doubts. His opponent began to think, had he moved ok? Would he find a tactical weakness? At least they had left known territory and they weren now at a stage more interesting. He hoped to preserve a solid pawn structure to go throught mid game to the end.
Although white and black pieces have 20 movements to choose at the beginning of the game, only are good a few of them. These are the first moves made in each game of the tournament. The density reflects the number of times the movement was done.
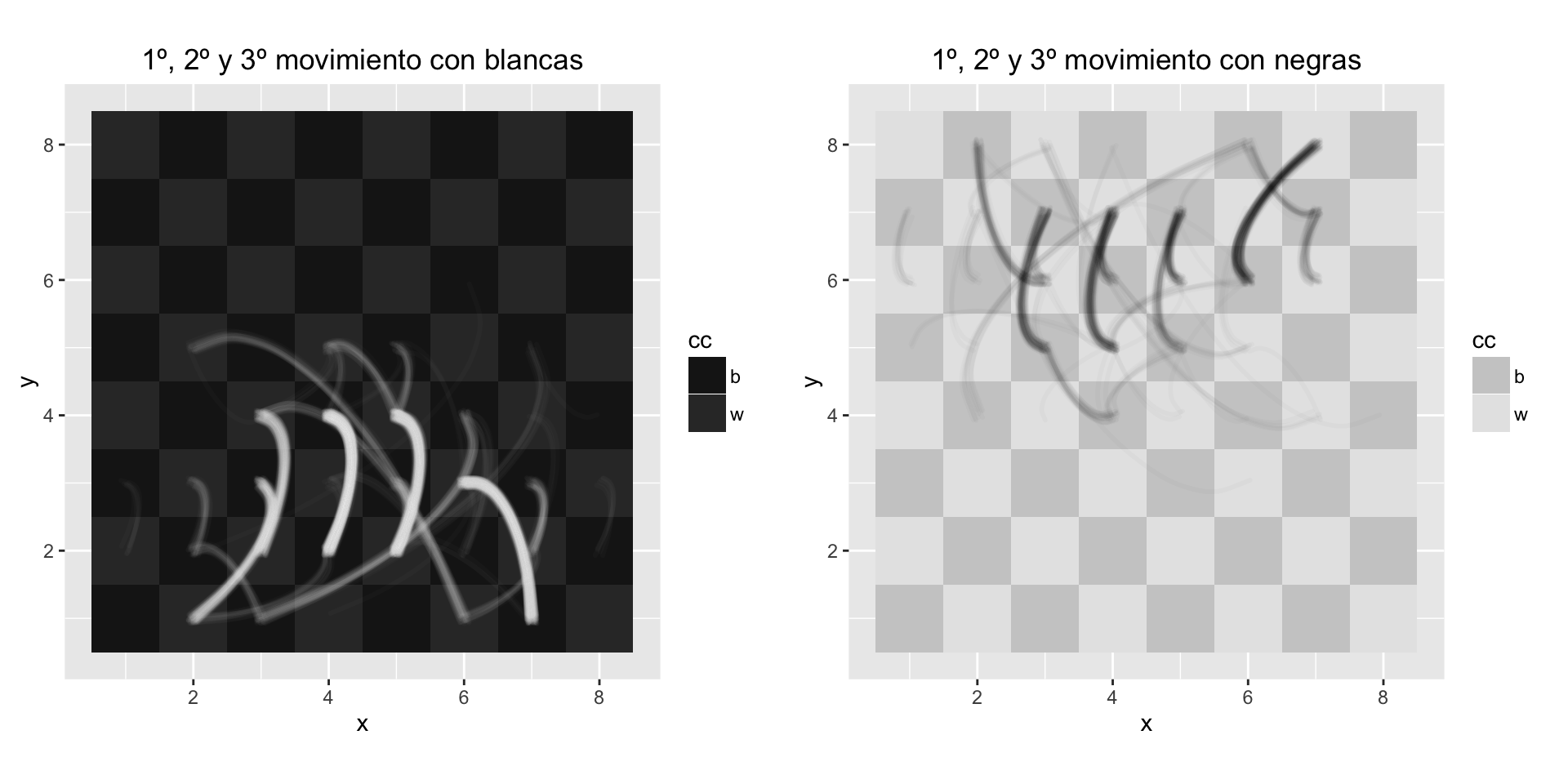
To see what happens in a chess tournament in which there are dozens of people playing simultaneously, you can use this board in which are drawed the first movements of all games simultaneously. It's like watching overlapping all games on a single board, thought and stress of many people reduced to a few seconds.
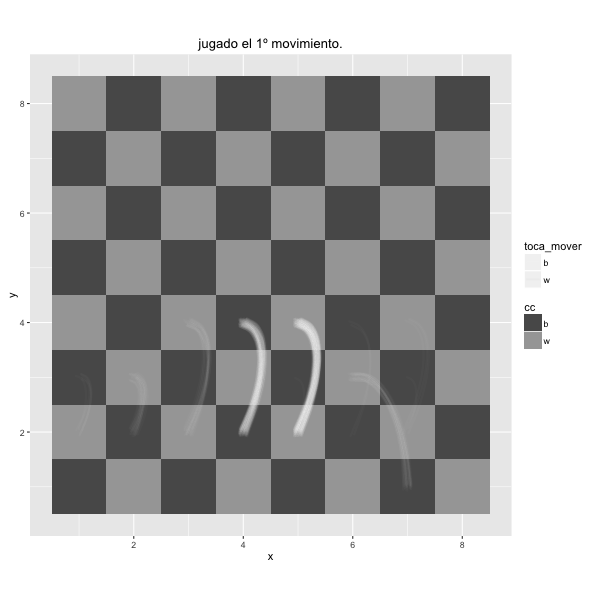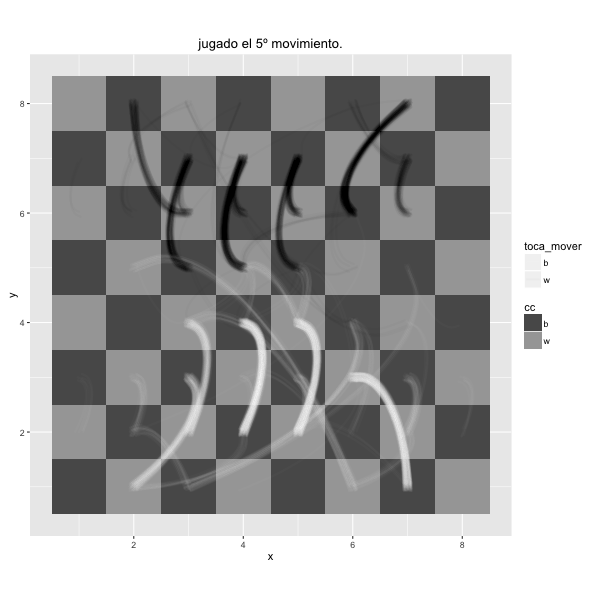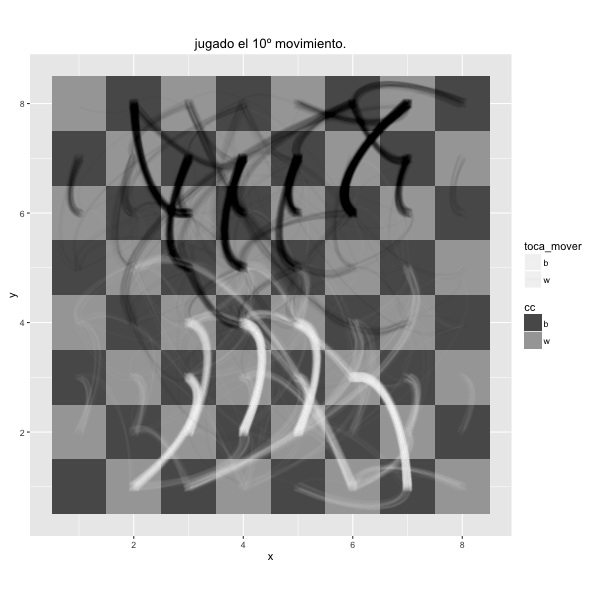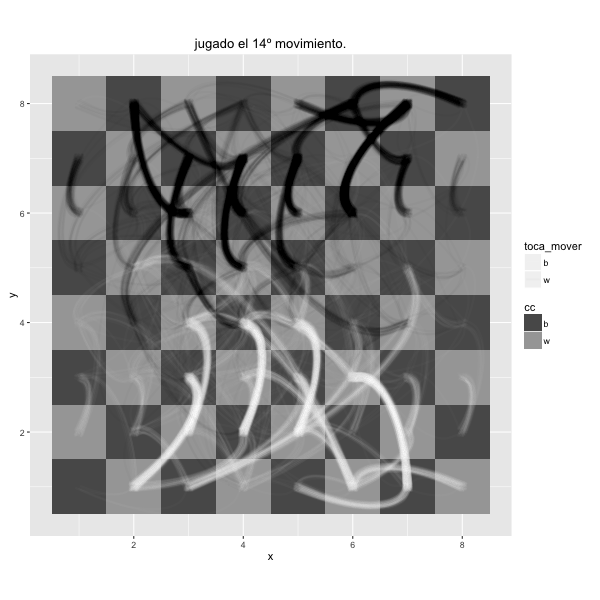
While his opponent was thinking he had time to observe him. He was a few years older. It was not the first time he saw him, but he could not place it. He was biting his nails and touching his ear with the left hand. After a few moves, he managed to remember. They went to the same school of english but never had greeted. Nevertheless, he felt contempt for him because of a comment he had heard him a few months.
The events had happened as follows: one day he was leaving his class when entered two older boys, they collided with him fortuitously as they passed in the hallway, he muttered "sorry" but they did not respond, They were surprised, as to make it clear that he was invisible to them, and when they were leaving one of them exclaimed, laughing, "greenhorn!".
Really, he did not know who had uttered the word, his opponent or his friend, but it mattered little. Now he had an ethical reason to beat him. "All right! Let's see who is the greehorn now!" thought while making a move. It would be great to win and see him feel the pain of his sophisticated revenge.
Middlegame
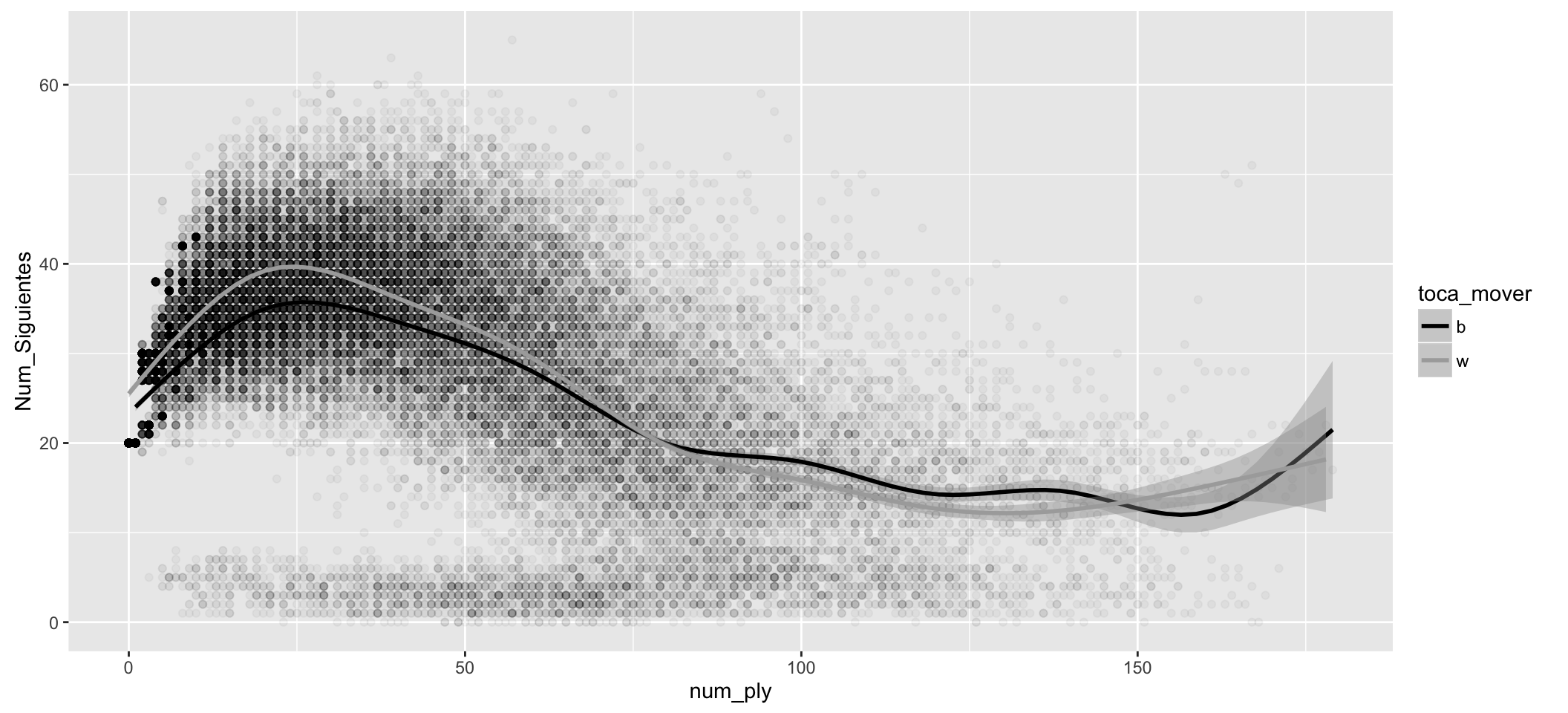
The following diagrams show the average trend of all games. The idea I want to capture is as follows:
- At any time, a player can choose between a small set of legal moves.
- This number of possible moves, reflects to some extent the degree of freedom a player has. Intuition would suggest that whoever has more freedom, will have more probability to have the best movement.
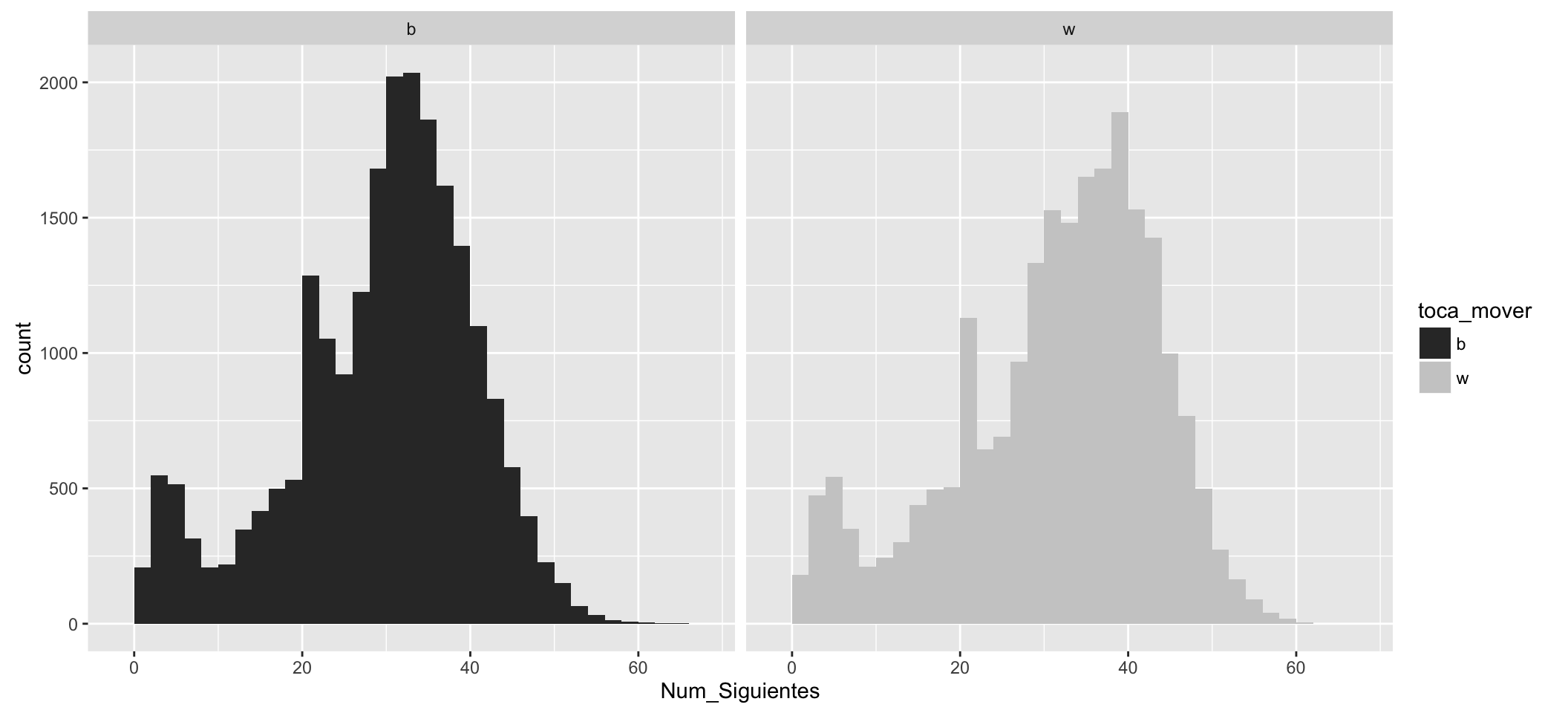
In the following diagrams, the cloud of points reflects the number of possible moves that had the players on each ply. The first diagram reflects white and black combined. The next two reflect the same information separately. Keep in mind that white plays in odd movements and black in even.
Dividing the movements of the white and black in their respective diagrams:
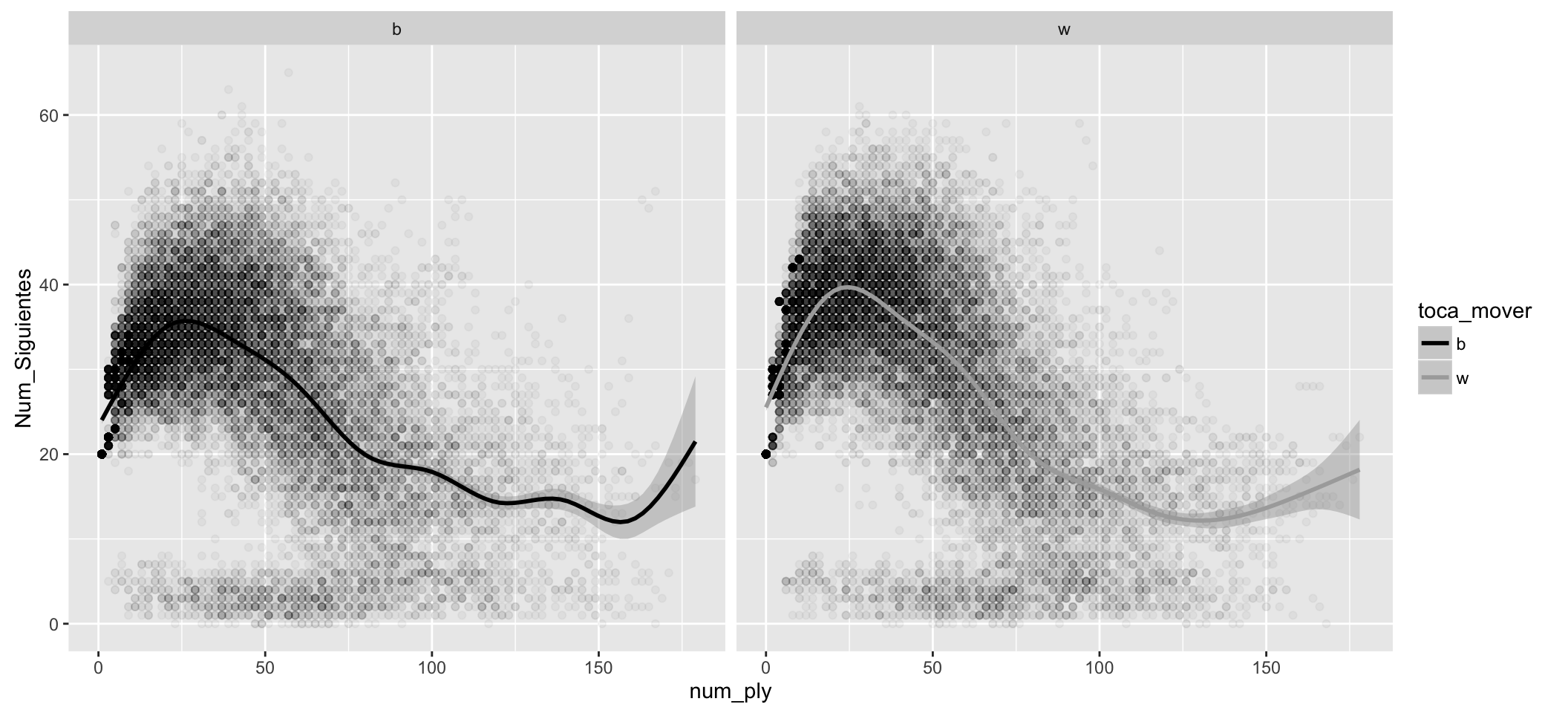
The above diagrams show several things.
- White, on average, have more possible moves at the beginning of the game.
- At the beginning of the game there are 20 possible moves in each position for both, white and black (moving pawns 1 or 2 positions and the four possible movements of knights).
- The maximum possible movements (the maximum average is approx. 40, for white) and it is reached in 25 to 30 ply.
- There are positions with more than 50 or 60 possible moves, however, they are very few.
- The cloud of points becomes lighter as plys advance. This is logical, the games are finishing.
- From the ply number 50 approx. White and Black begin to match the possible moves, and on average, they are below 20 (They are positions with few pieces on the board).
- There is a cloud of points more or less uniform over all plys with less than 10 possible movements. This cloud corresponds to the Checks received, leaving little chance to choose the movement.
The same thing, we can see in a 3D diagram in which the density of the points is replaced by the height. Each color is in his own tab. If it is switched, the diagram shows that the white is slightly shifted to the background, to have more possible moves in each position.
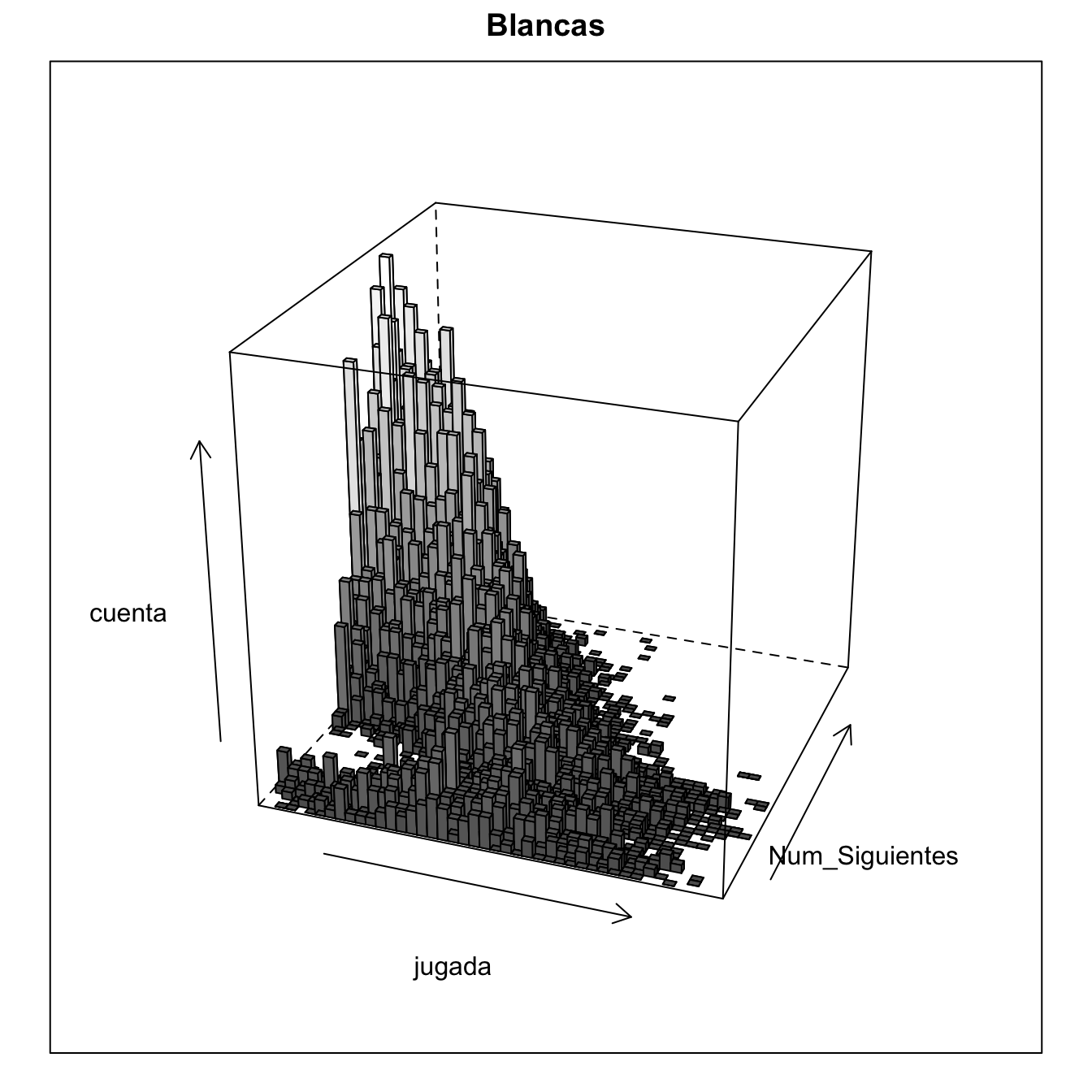
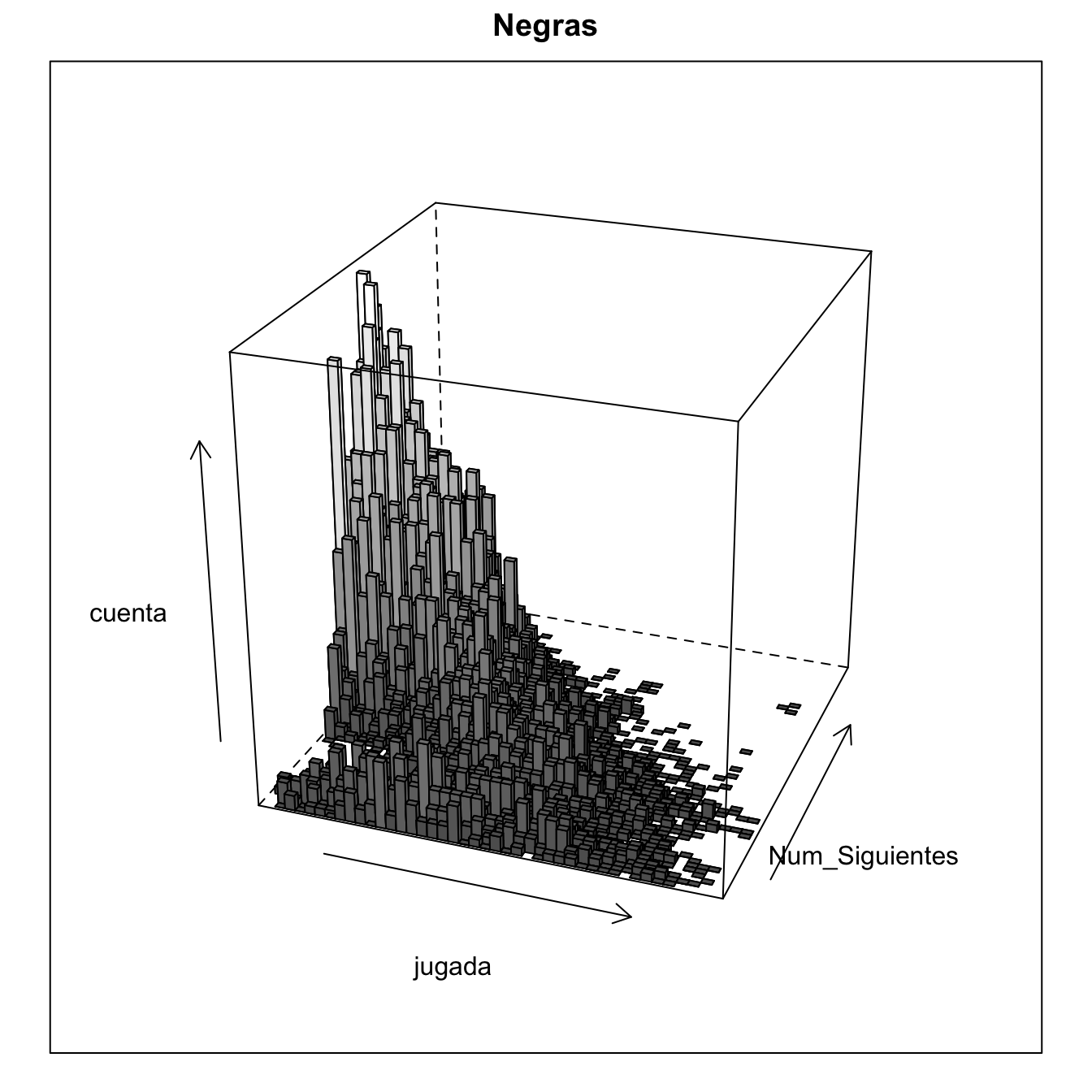
Number of positions in which there are a number of possible next moves.
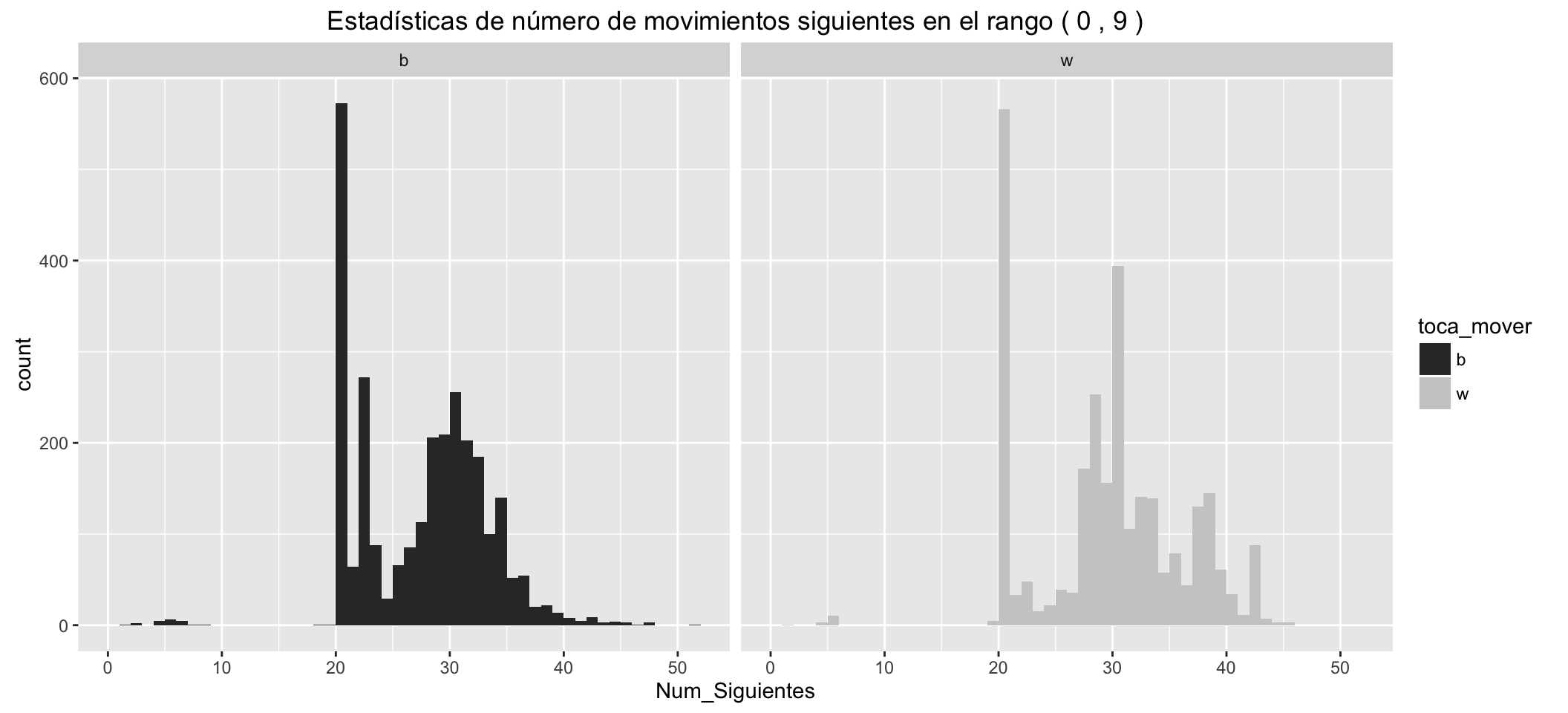
I want to further deepen this idea of the possible moves for a given position. In the following tabs, I have grouped positions in groups of 10 and shown cuts of each group in terms of possible moves, also displaying the information of the mean, median, maximum, minimum and quartiles.
 Statistics of number of possible next moves for White:
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 24 | 33 | 31.02 | 40 | 61 |
Statistics of number of possible next moves for black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 22 | 31 | 28.92 | 36 | 65 |
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 24 | 30 | 29.11 | 33 | 45 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 22 | 28 | 26.97 | 31 | 51 |
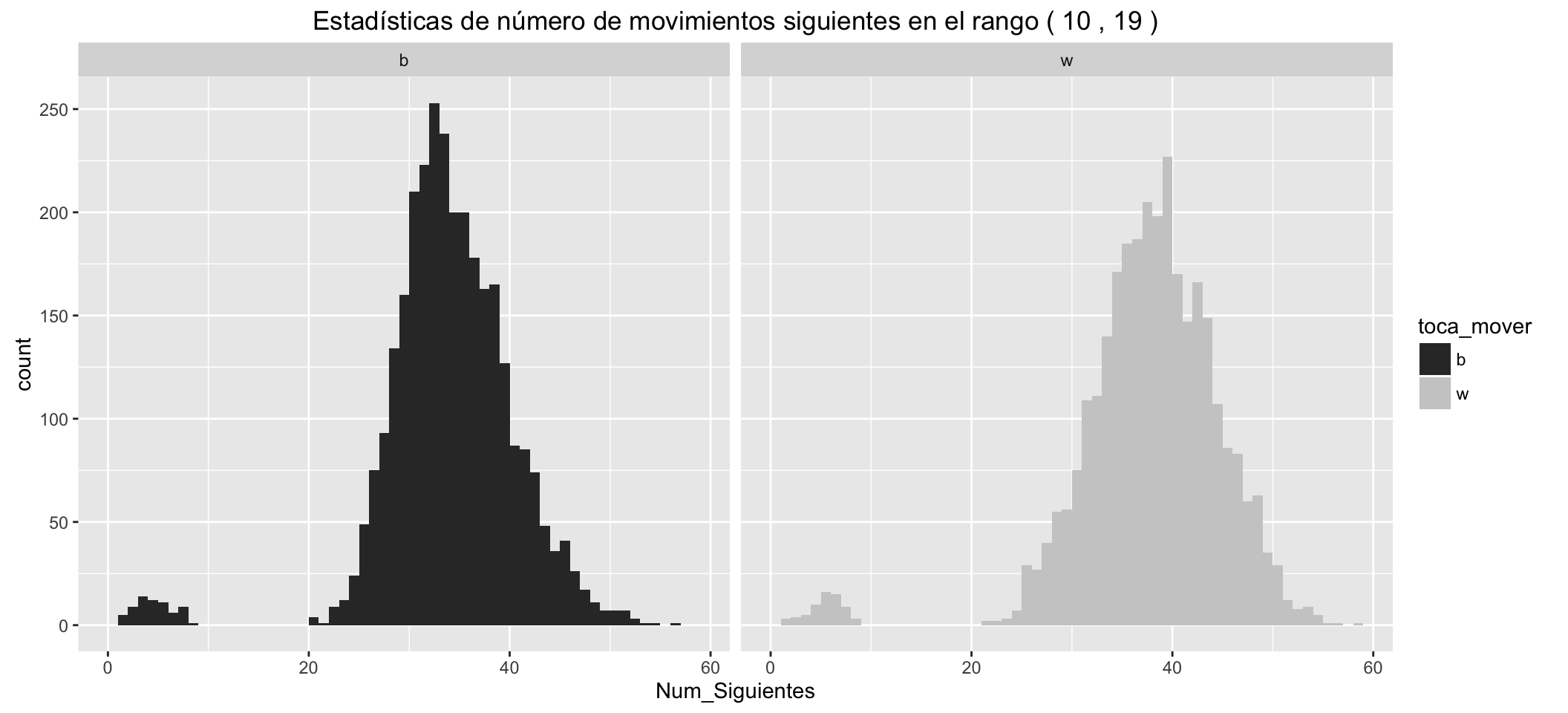
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 34 | 38 | 37.23 | 42 | 58 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 30 | 33 | 33.45 | 37 | 56 |
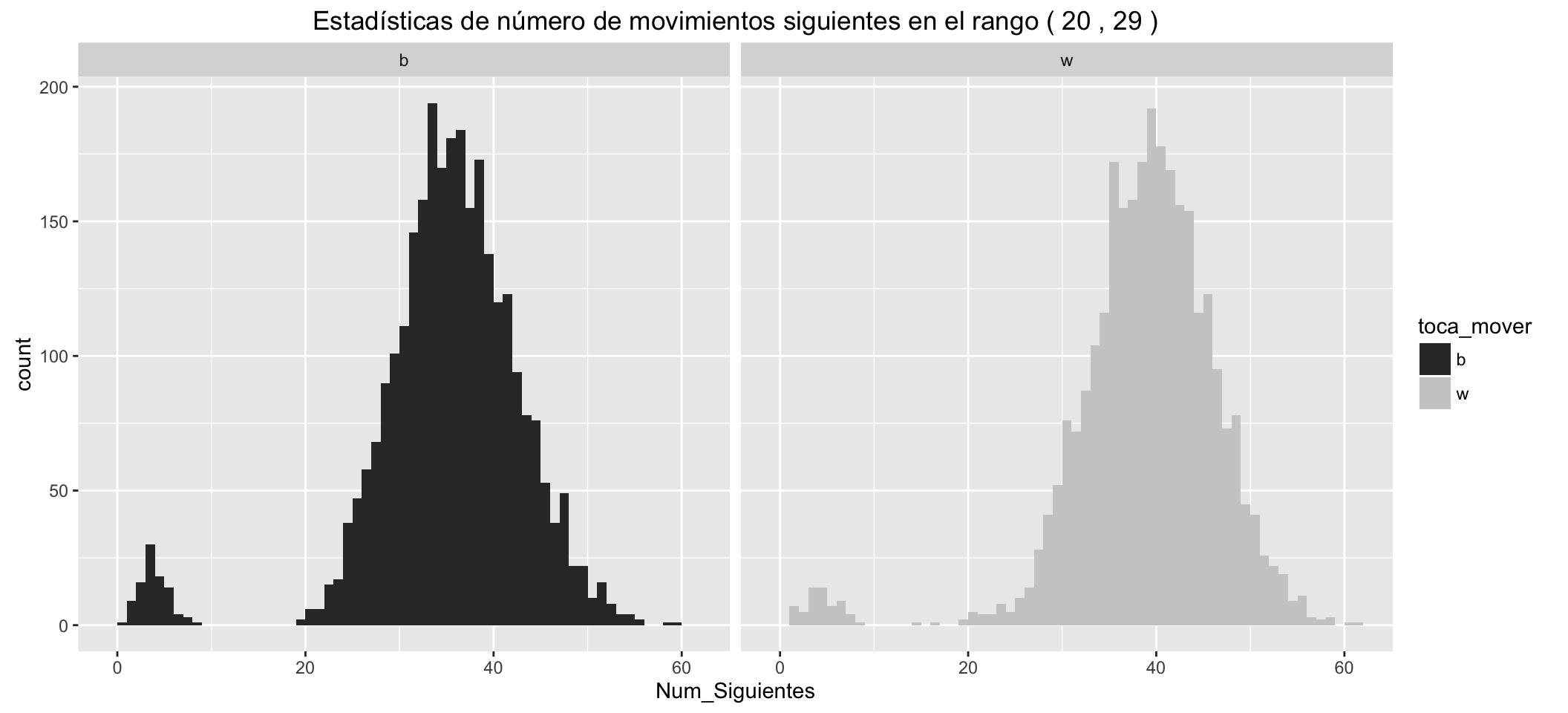
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 35 | 39 | 38.35 | 43 | 61 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 31 | 35 | 34.57 | 40 | 59 |
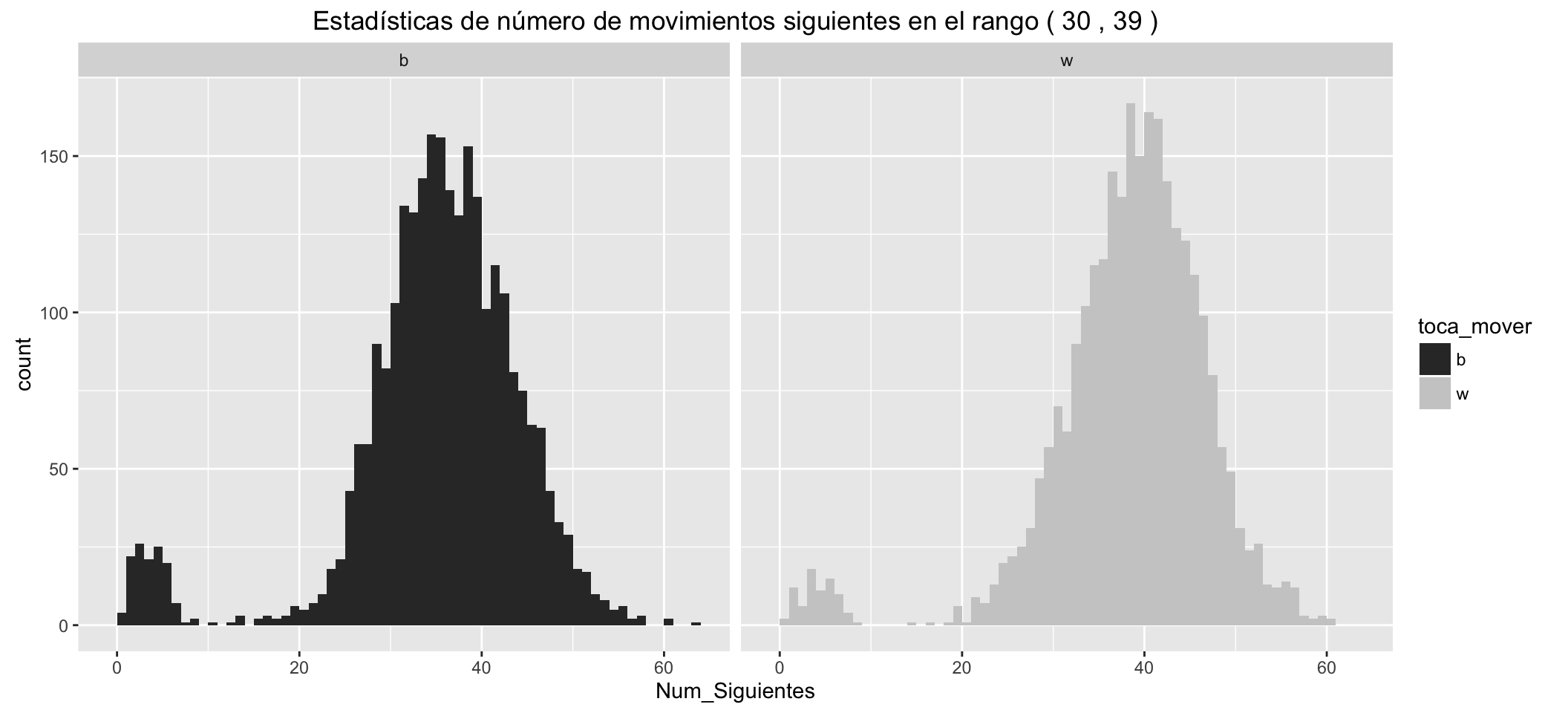
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 34 | 39 | 37.84 | 43 | 60 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 31 | 35 | 34.62 | 41 | 63 |
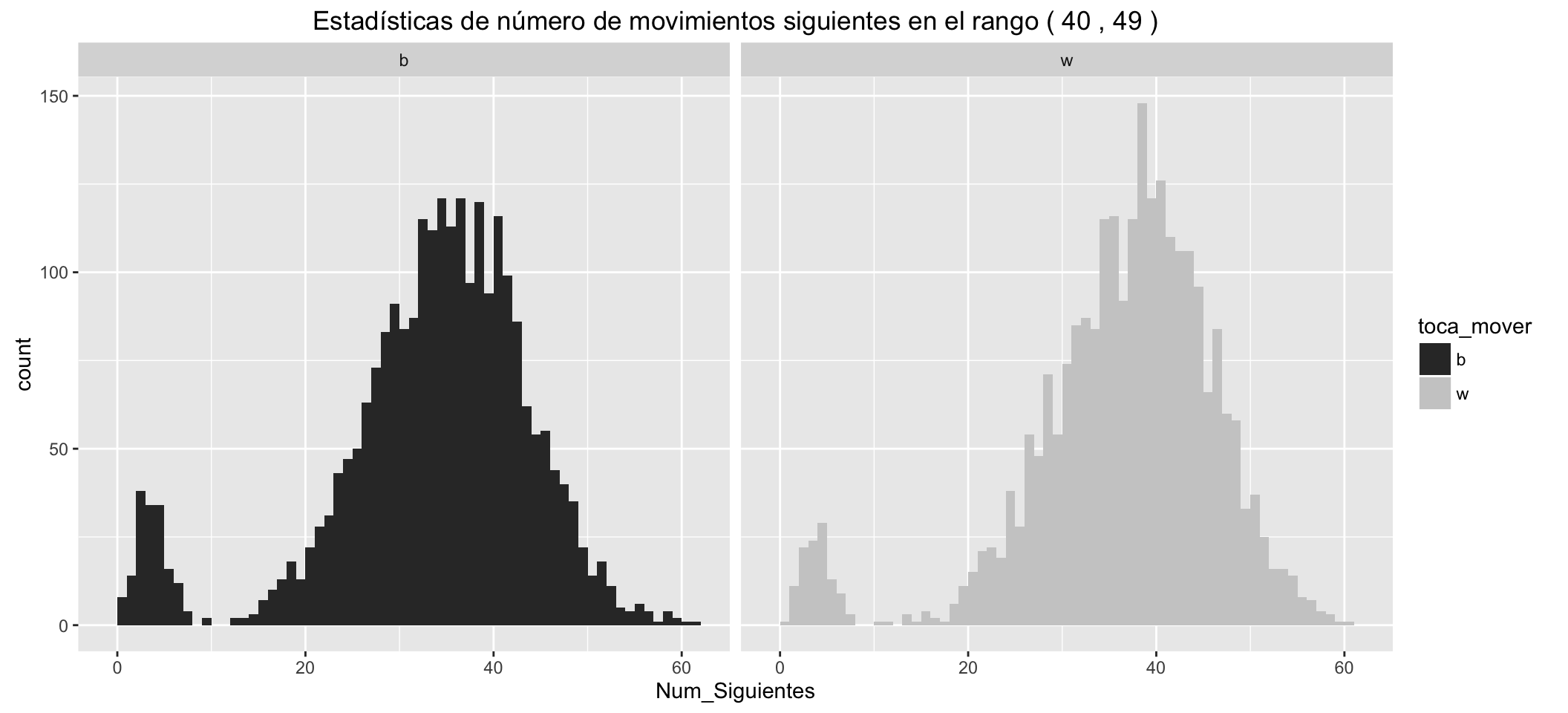
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 31 | 37 | 35.81 | 43 | 60 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 28 | 34 | 32.84 | 40 | 61 |
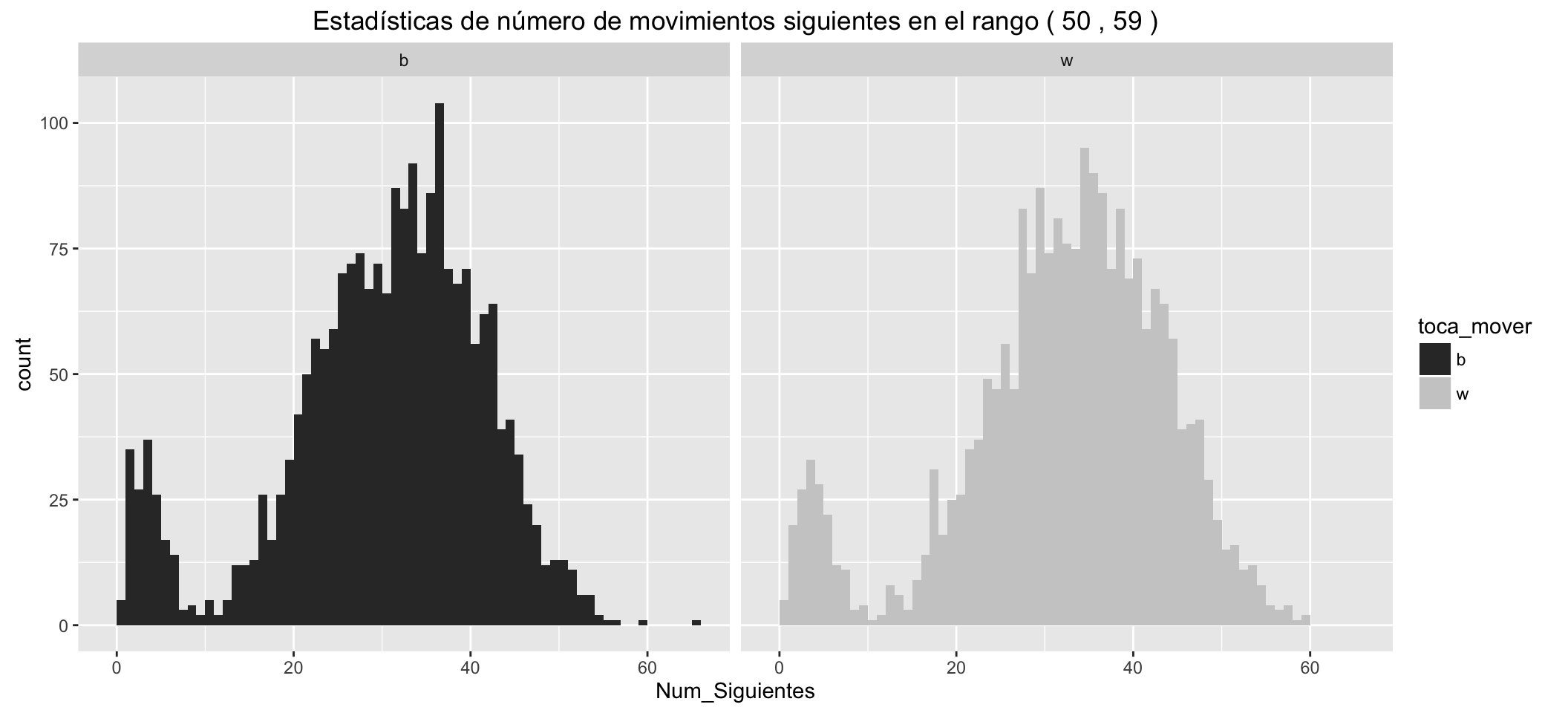
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 26 | 33 | 31.65 | 40 | 59 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 24 | 31 | 29.77 | 38 | 65 |
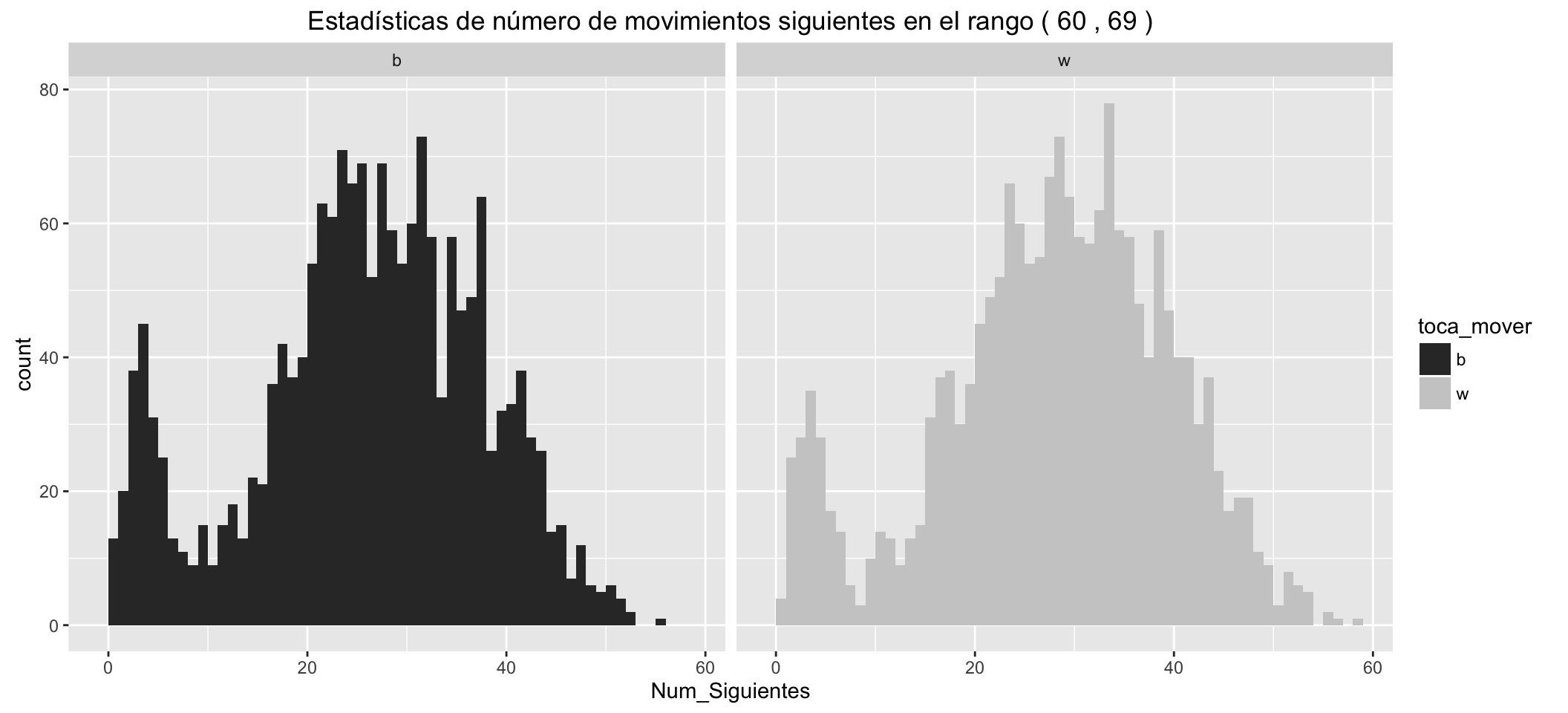
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 21 | 28 | 27.45 | 36 | 58 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 19 | 26 | 25.44 | 34 | 55 |
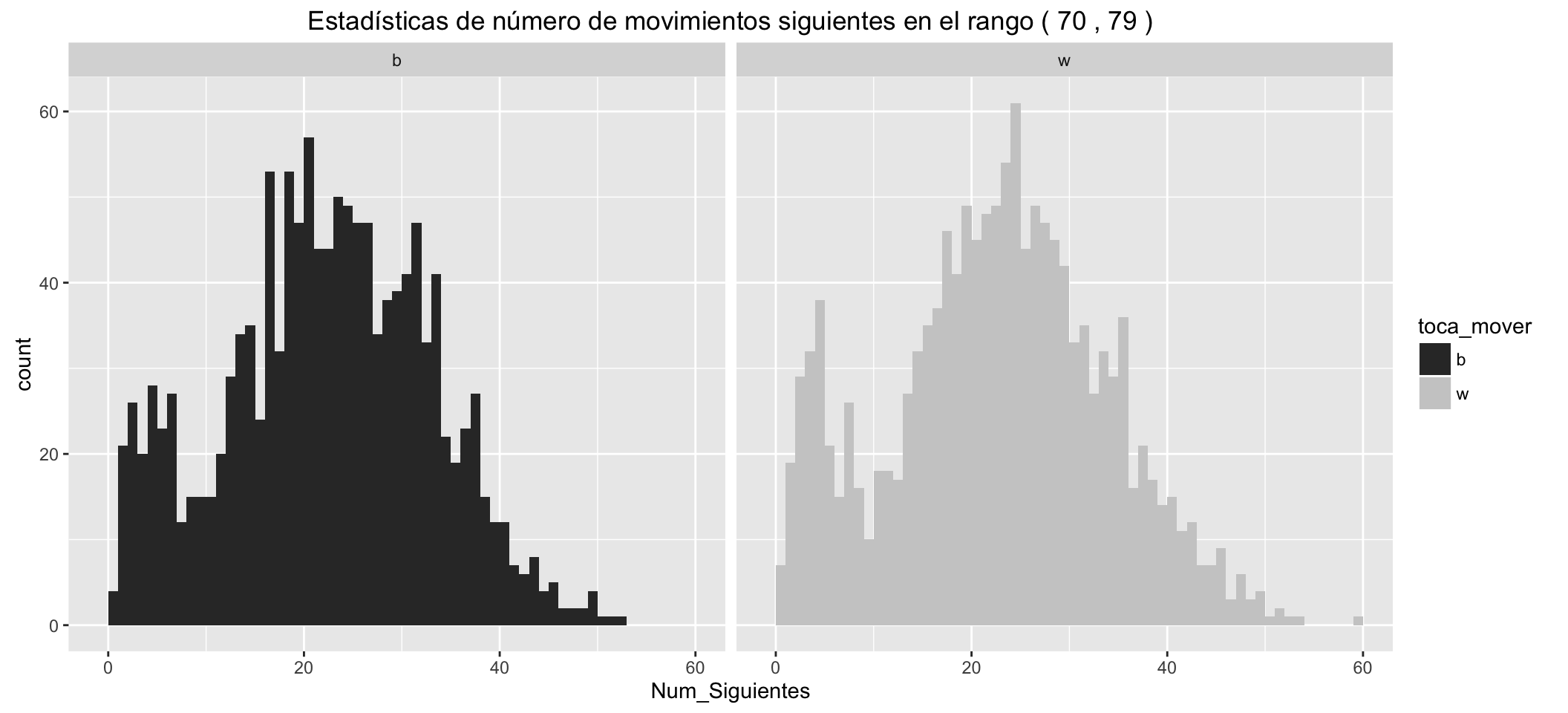
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 15 | 23 | 22.14 | 30 | 59 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 15 | 22 | 21.83 | 30 | 52 |
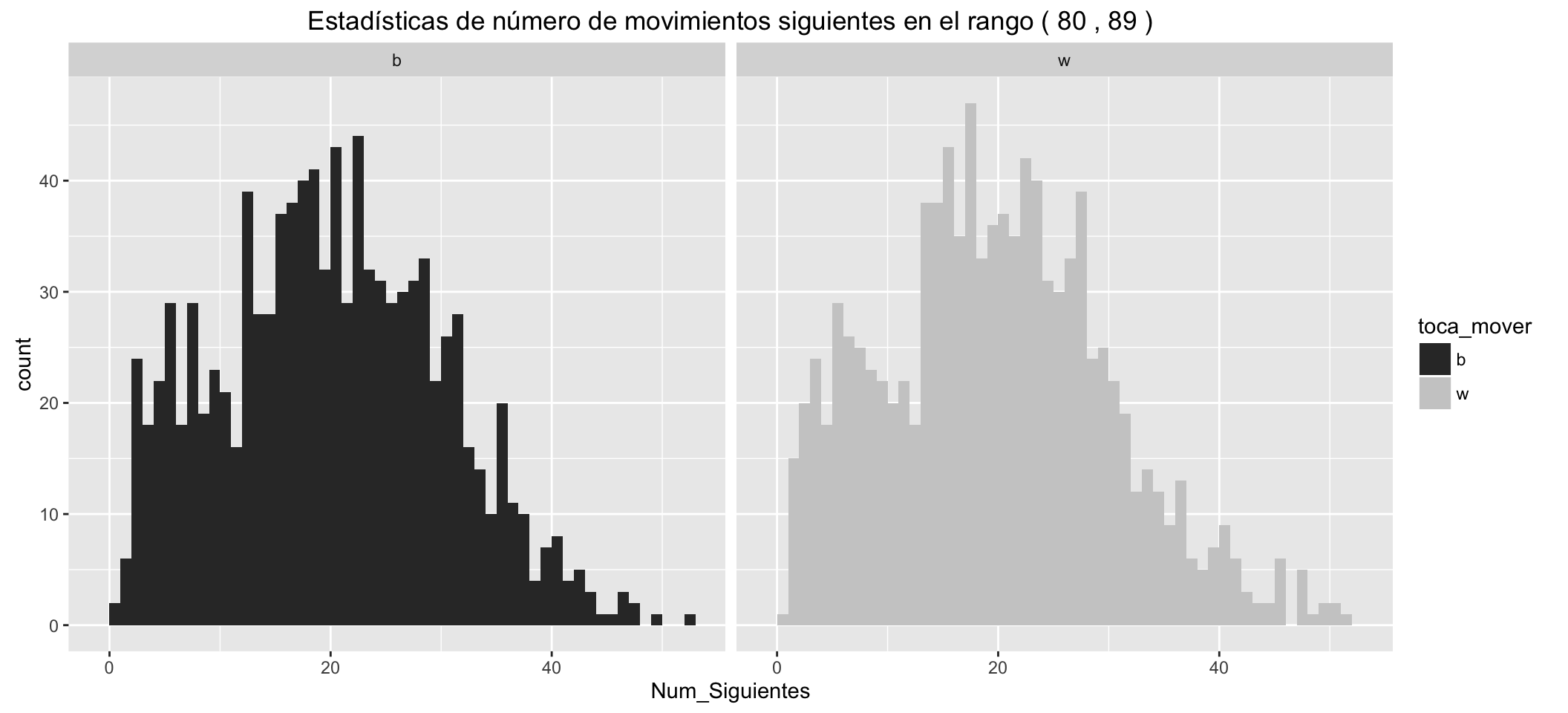
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 12 | 19 | 19.3 | 26 | 51 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 12 | 19 | 19.55 | 27 | 52 |
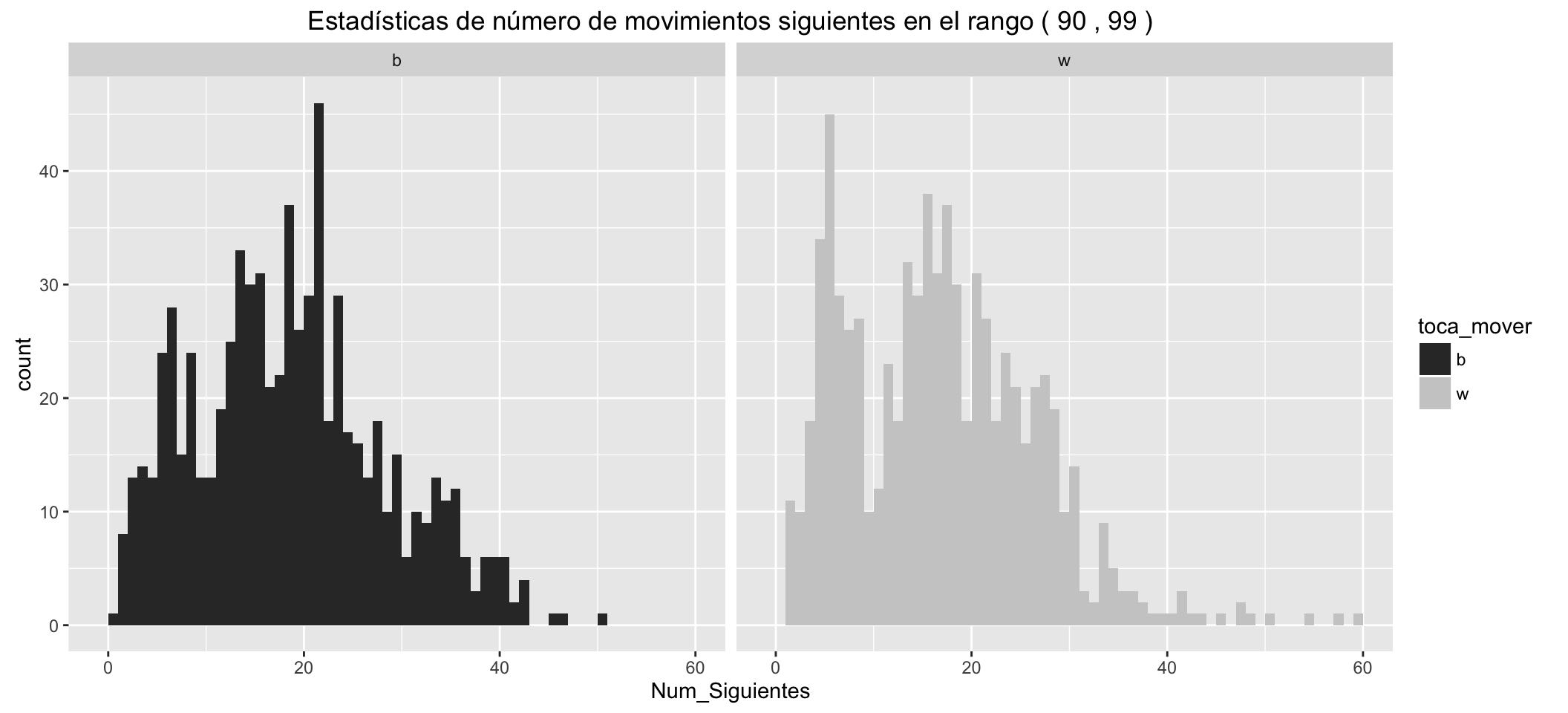
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 8 | 16 | 16.34 | 23 | 59 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 11 | 18 | 18.15 | 24 | 50 |
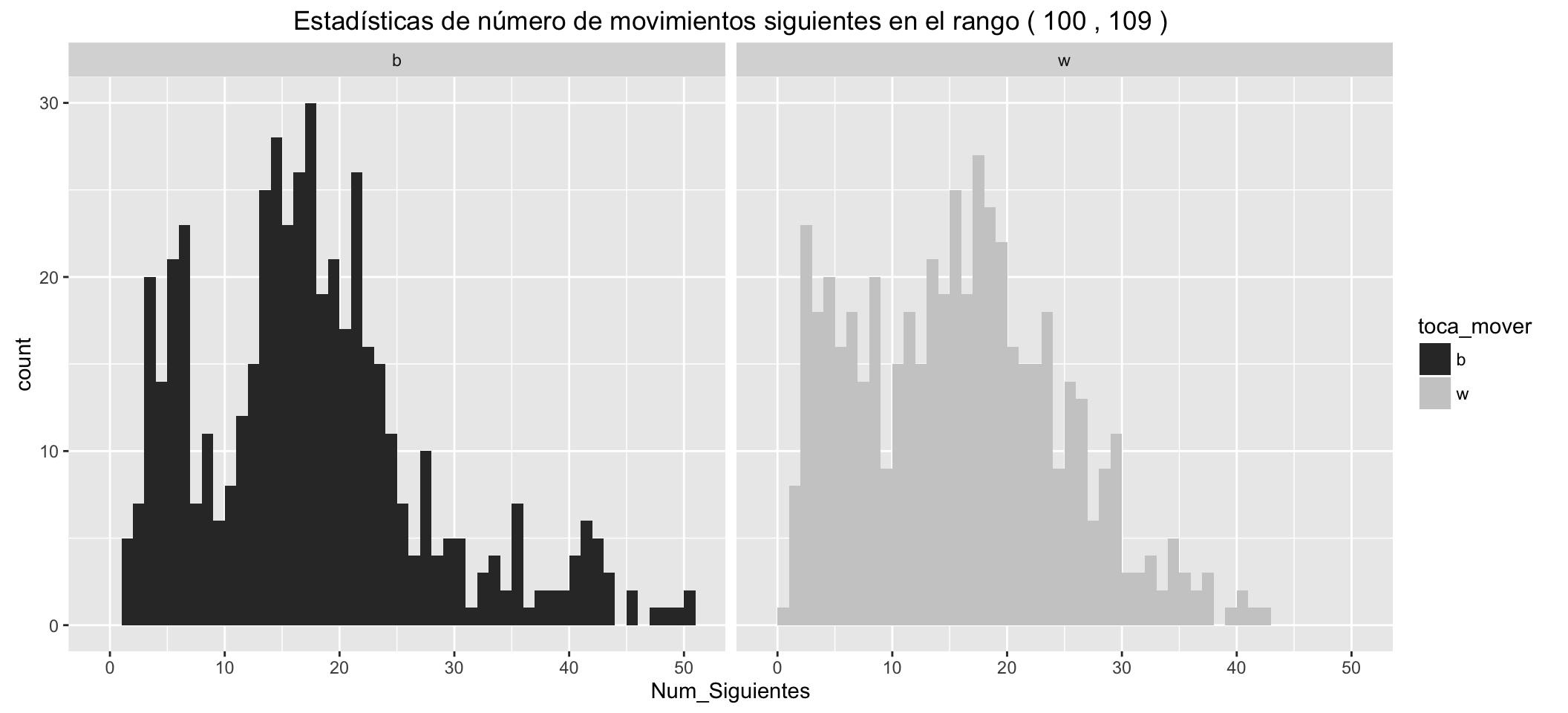
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 8 | 15 | 15.4 | 21 | 42 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 11 | 16 | 17.16 | 22 | 50 |
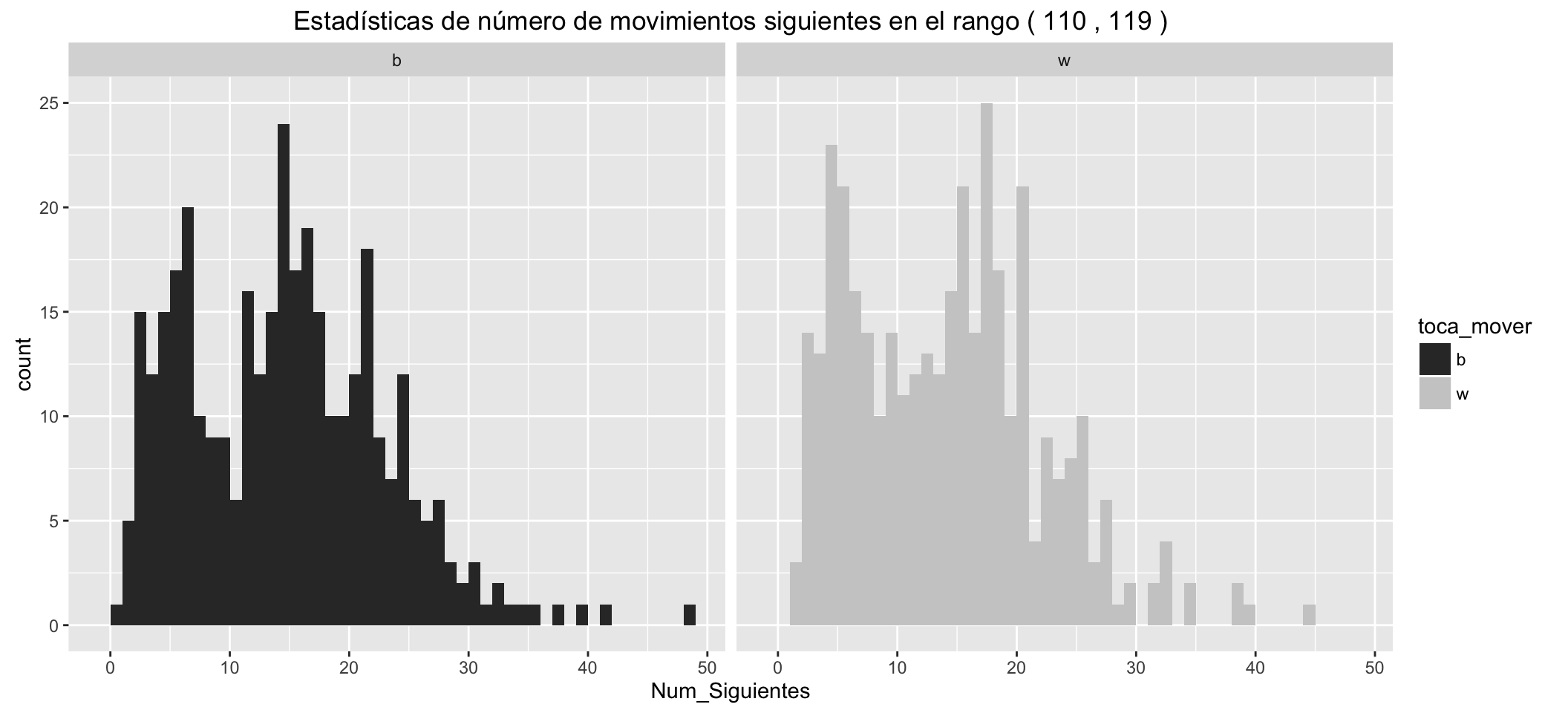
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 7 | 14 | 13.68 | 19 | 44 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 7 | 14 | 14.16 | 20 | 48 |
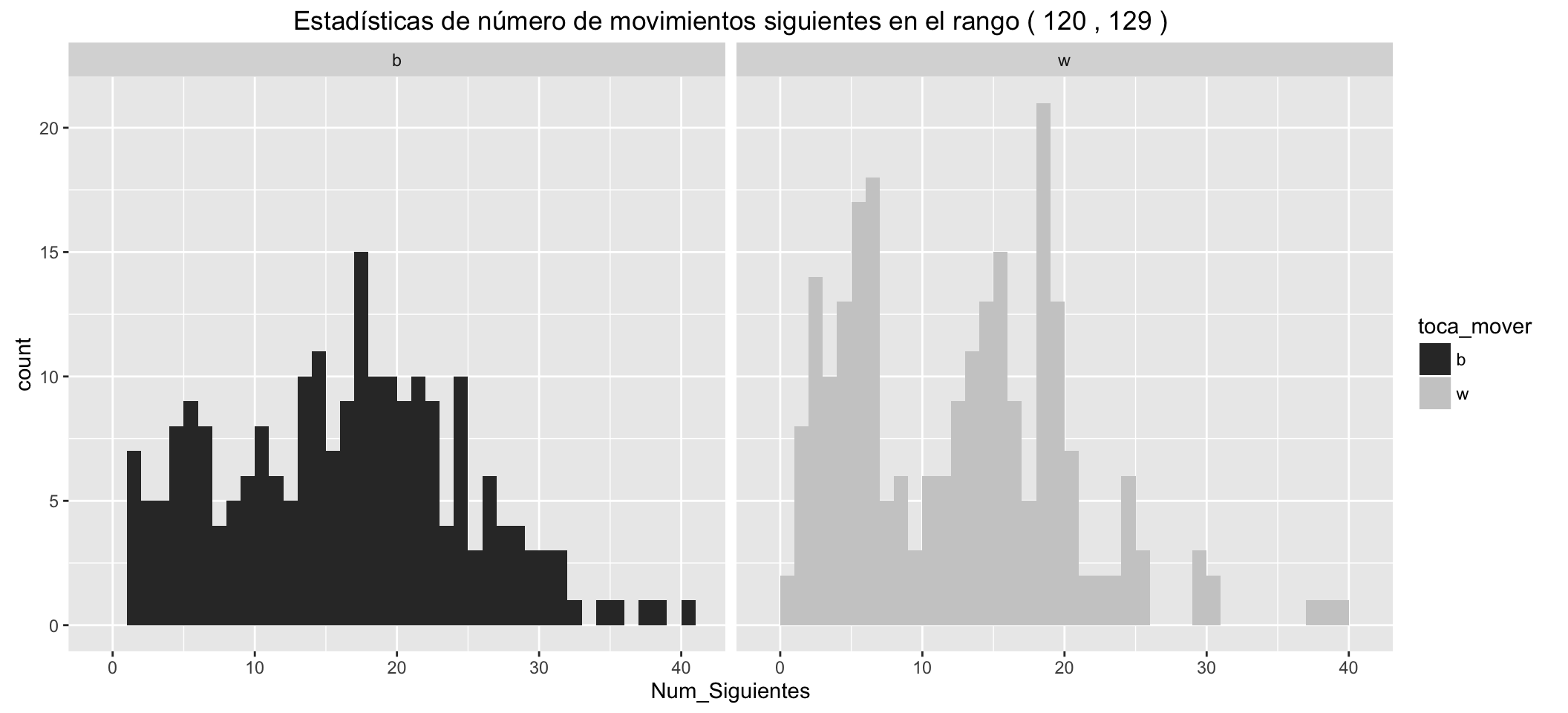
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 5 | 12.5 | 12.01 | 18 | 39 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 9 | 16 | 15.77 | 21 | 40 |
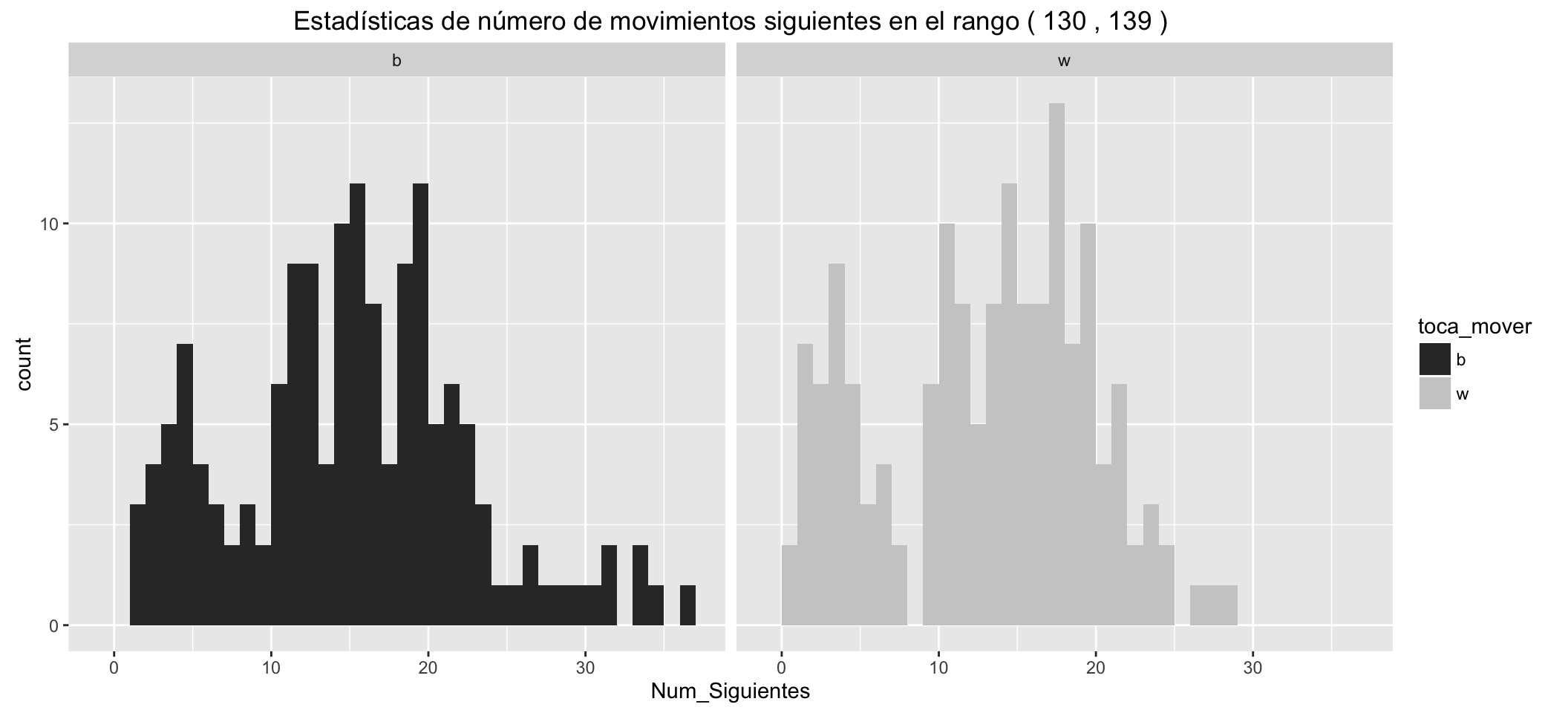
Statistics of number of possible next moves for White:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 7 | 14 | 12.52 | 17 | 28 |
Statistics of number of possible next moves for Black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 10 | 15 | 14.67 | 19 | 36 |
It can be seen than:
- The small groups of movements with Check, separated to the left.
- White has, in the different statistics, an advantage over black of about five more possible movements in the early stages of the game.
- These advantages are reduced as the game advances.
He looked at the board and resigned himself to the harsh reality. To be his first official game with black against a rival with elo ... He guarded his position. To reach the fifty ply was not available to everyone.
Some tables had finished, and the players walked in silence, watching other games. They were nearing the end, they still had the same pieces, exchanges were fair, he had managed to see a trap, but the initiative remained at the White side. For a fleeting moment he thought of offering a draw, what he could lose!, but he dominated his pride, he still expected to win. The last two knights fell, and free remaining pawns. So was his opponent who offered him draw.
Ending
The statistics at the end of the game, distinguishing white and black, are as follows in this tournament. The number of games that terminated winning at each ply is displayed. Matches that are to the right are the longest (in number of plys).
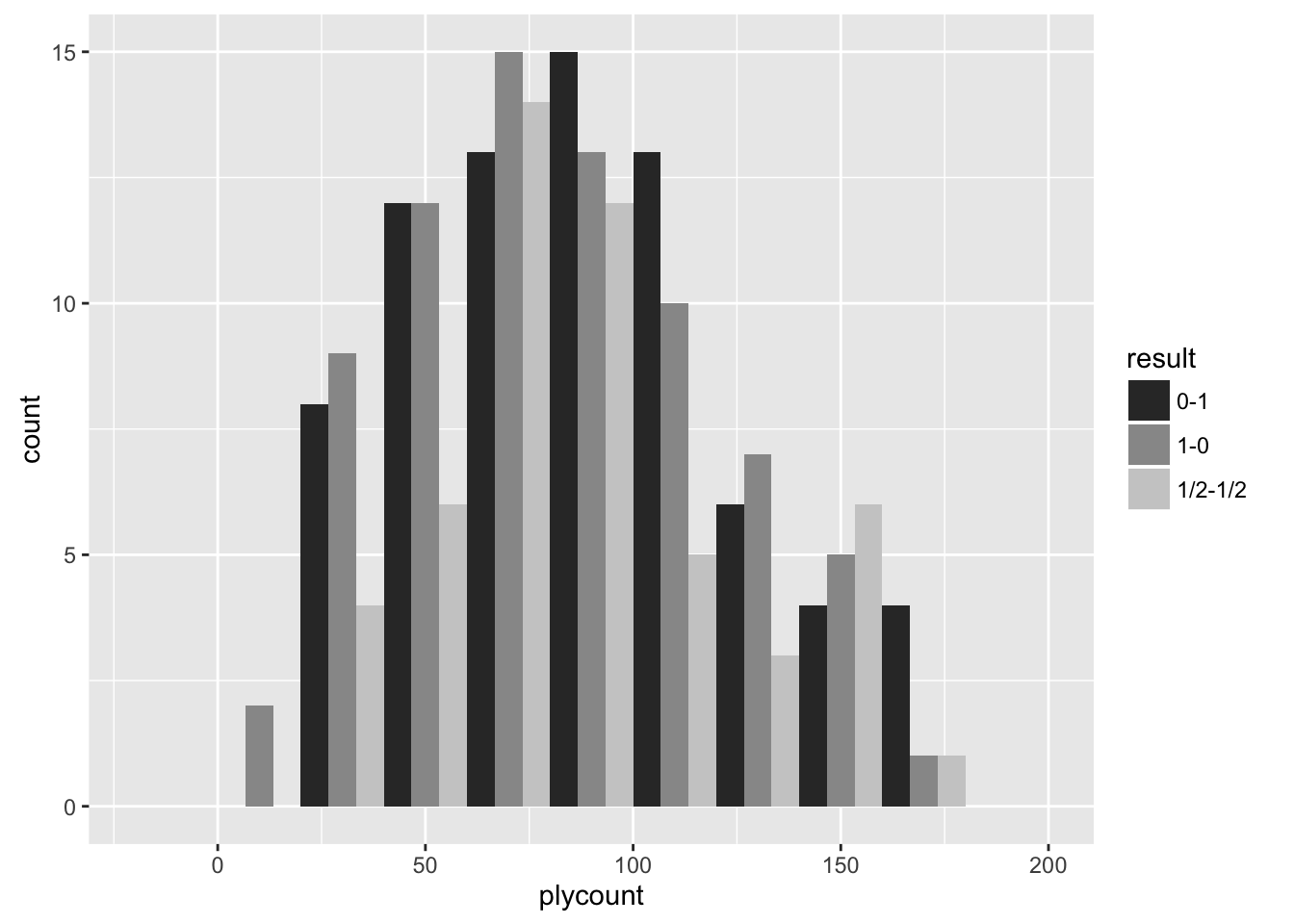
Statistics of games won by white:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | NA’s |
|---|---|---|---|---|---|---|
| 1 | 51 | 69 | 71.94 | 89 | 167 | 24 |
Statistics of games won by black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | NA’s |
|---|---|---|---|---|---|---|
| 23 | 58 | 72.5 | 79.36 | 97.25 | 168 | 25 |
Statistics of games ended with draw:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | NA’s |
|---|---|---|---|---|---|---|
| 20 | 67 | 80.5 | 86.47 | 102.8 | 173 | 10 |
Data shows that proportionally, white wins in shorter games. Black needs more moves to win, and even more is required for a draw. At least in this tournament.
Is it related in any way to the number of possible next moves? If we look at the statistics of the victories of white against black and vice versa:
Next possible movements in games won by white
for white:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 27 | 35 | 33.33 | 41 | 61 |
for black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 21 | 30 | 27.51 | 36 | 58 |
Next possible movements in games won by black
for white:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 21 | 31 | 28.95 | 38 | 60 |
for black:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 25 | 32 | 30.58 | 38 | 65 |
Without going into a formal statistical analysis, it appears that, on average, when white wins, they have 5 more movements to choose from in each ply.
By contrast, in the games that black wins, they have, on average, 1.5 more moves to choose from, and we must take into account that, for the first movements, Black has to compensate for a disadvantage of about 5 possible moves.
Then, the data seem to confirm that, to some extent, the victory in the games, is related to the number of possible moves in each movement. We could study the correlation and establish a model to predict the victory of one or the other throughout the game, but that will have to be in another article.
Epilogue
One last thing, when the game ends where the king? The following diagrams, reflect the positions of the kings castling. It seems that both, in number of games, and in percentages, castling improves the chances of victory.
Lugar de finalización de los reyes
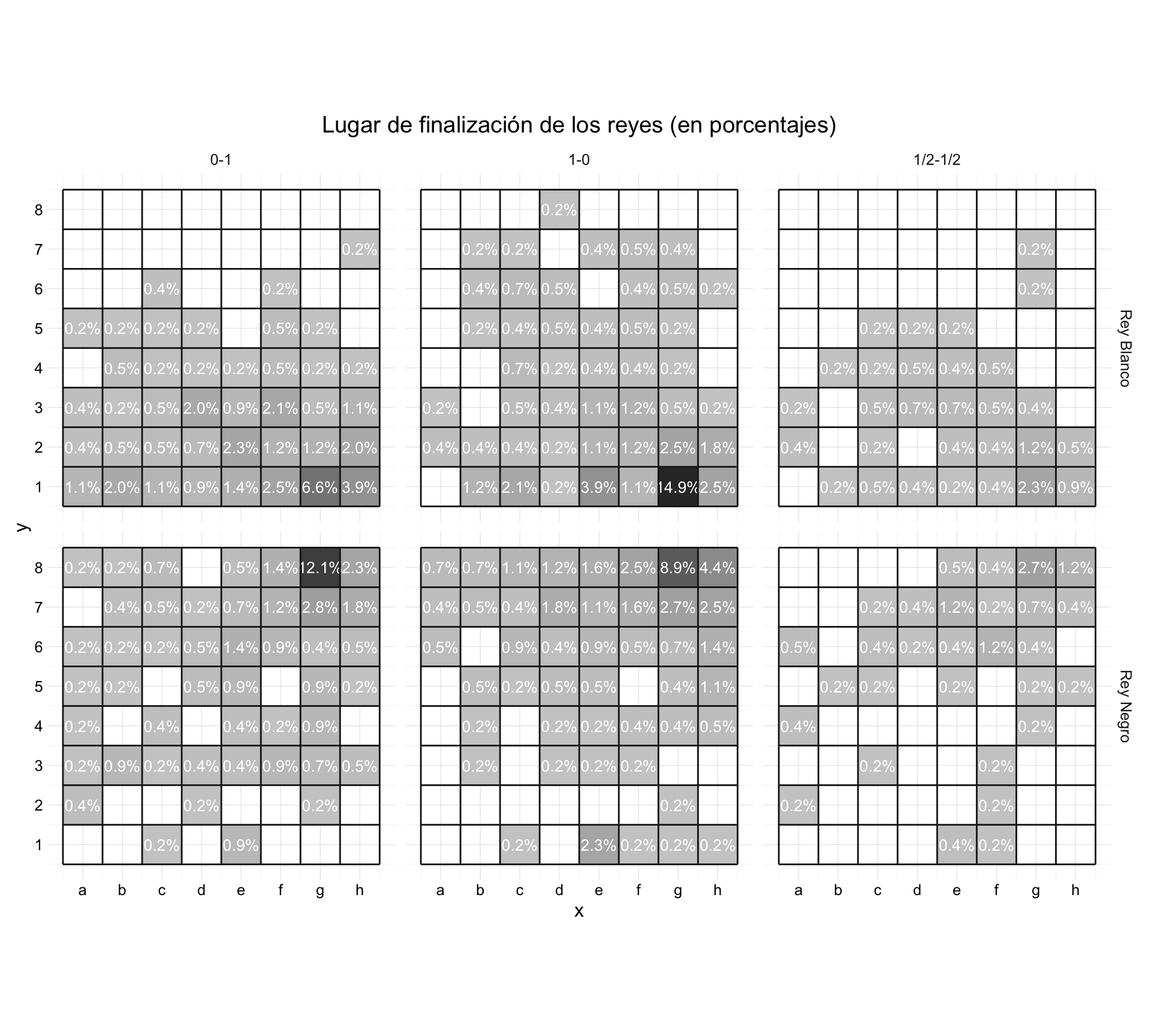
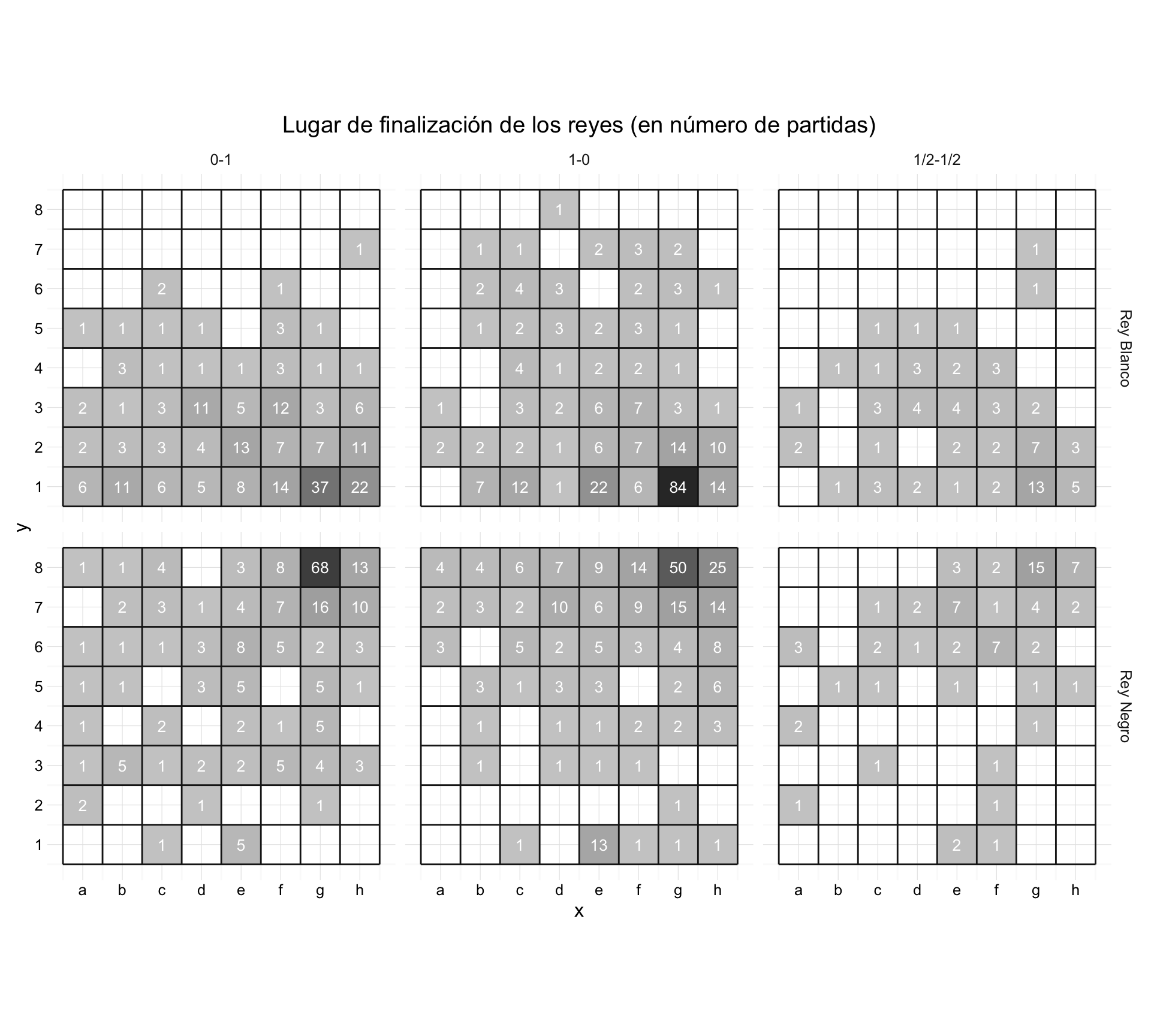
The other showed no sign of remind him. He beat his pride and accepted. "Do you play since long ago?" He asked. "It is my first official game," he replied. "Congratulations! You played very well. " He smiled, the offense was forgotten. He looked at him and honestly answered "Thank you", adding, "you too".
The end
Links
For more information on the concept of mobility in chess: Chess Programming Wiki / Mobility
Thanks
I want to thank Joshua Kunst for his package for R rchess and for his ideas, which I borrowed.