Torneo de Ajedrez (un análisis y un relato)
Este artículo es, a la vez, un relato y un análisis en R sobre un Torneo de Ajedrez real. Sin embargo, aunque cada partida, cada jugada y cada resultado, sean reales, las breve historia narrada es ficticia.
El análisis completo realizado en R, junto con los conjuntos de datos, está publicado en github en este enlace.
Apertura
Miró al techo de su habitación por última vez antes de levantarse. No había pegado ojo, al menos así se lo parecía, su cerebro no dejaba de repasar aperturas, tácticas, estructuras de peones, celadas y finales con diversas piezas.
Seguramente había dormido más de lo que pensaba, al menos no se sentía cansado… O quizás, simplemente eran los nervios.
Durante la última hora, cuando la luz comenzó a filtrarse entre las cortinas, había añadido a su juego mental un tablero imaginado sobre el techo en el que las piezas se movían a su voluntad.
Hoy era la primera vez que iba a competir en un torneo oficial, y las manos le sudaban.
Algunos datos
Para el análisis del torneo disponía de un fichero con todas las partidas desarrolladas. De este fichero eliminé aquellas que tenían errores por diversas causas. Por ejemplo:
- No se habían disputado por ausencia de alguno de los contrincantes.
- Error en los movimientos, bien por que el número de jugadas no cuadraba con el número indicado en el fichero, bien por faltar jugadas en el pgn.
Después de depurar la información, eliminé los datos personales, el nombre y lugar del torneo, y los nombres de los jugadores de cada partida, manteniendo la distinción de cada uno de ellos durante la anonimización.
El dataframe resultante contiene 562 partidas, que son las que he utilizado en el análisis.
El pabellón del polideportivo en el que se jugaba el torneo estaba preparado para la ocasión. Habían desplegado las mesas en cuidada formación y en cada una de ellas había un tablero de cartón y un reloj. Esto le recordó las reglas que acababa de estudiar “Se entiende por caída de bandera la finalización del tiempo asignado a un jugador”. Una de las cosas que más le preocupaban era agotar el tiempo de juego, de nada le servía jugar más o menos bien, si lo consumía completamente. Aunque ello significara acabar una partida sin recibir mate.
Se podía decir que el ambiente que se respiraba en el pabellón era muy parecido al de un templo de oración. Saludó a varios conocidos, pero no quiso entablar conversación, eran los momentos previos al combate y todos requerían concentración.
Buscó en el panel cual era su mesa y su partida. Le había tocado jugar con negras contra un elo 1600. Ahora vería si estaba preparado o no. Intentaría no caer en las trampas de una apertura, intentaría cerrar la posición, esperar, que el otro tuviera que esforzarse para ganarle.
Estos son algunos datos generales del torneo. Participaron 165 jugadores, con las siguientes victorias en cada caso:
| blancas | tablas | negras | desconocido |
|---|---|---|---|
| 260 | 76 | 225 | 1 |
Existe una partida que no tiene resultado conocido en el fichero (’*’ en notación pgn) por lo que no la tuve en cuenta para el análisis.
La distribución del número de movimientos de las partidas fue la siguiente:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | NA’s |
|---|---|---|---|---|---|---|
| 1 | 56 | 72 | 76.84 | 94 | 173 | 59 |
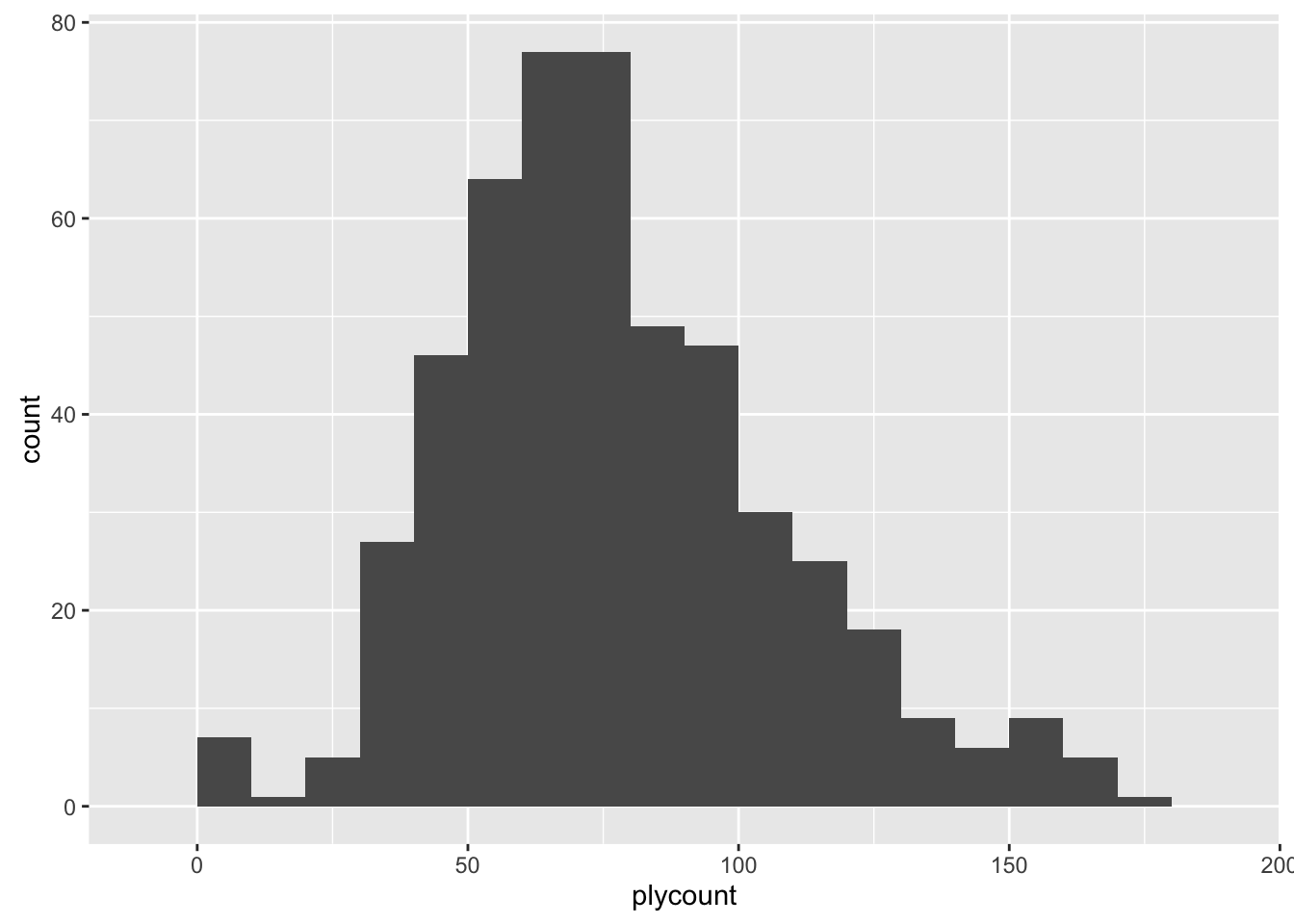
En este torneo, cada partida duró de media unos 77 movimientos, sin embargo, hay partidas que se alargan muchísimo más. Se puede observar que el sego del histograma es hacia la izquierda, el tercer quartil está en 94 movimientos. Solamente el 25% de las partidas dura más de 94 movimientos.
En el histograma hay un pico a la izquierda. Se corresponde a 7 partidas en las que solamente se produjo un primer movimiento, aparentemente son aquellas en las que el rival de las blancas no se presentó.
Se sentó pronto en su sitio, su oponente aún no había llegado. Miró a su alrededor, un mar de tableros y personas a punto de comenzar una batalla incruenta. Colocó su planilla a la derecha, equidistante a ambos bordes de la mesa, y el bolígrafo, en perpendicular, a dos centímetros de separación. Los demás, los que ya estaban sentados, desplegaban, a su vez, sus respectivas manías y tics.
El primer movimiento de las blancas había sido e4, “perfecto”, pensó, y respondió rápidamente con c6. Su rival continuó, sin pensarlo, con d4, a lo que él respondió igualmente con d5. Así continuaron durante unos cuantos movimientos más, incluido un intercambio de peones, hasta que se vio forzado a pensar. Su rival, que seguía respondiendo rápido, había hecho un movimiento desconocido para él, ¿sería una trampa? ¿Un fallo? O ¿la mejor jugada posible contra la defensa Caro-Kahn? Después de un buen rato calculando, respondió tratando de que el otro no adivinase su inseguridad. Su oponente comenzó a pensar, ¿había movido bien? ¿encontraría una debilidad táctica? Al menos había salido del territorio trillado y entraba ya en la fase del juego más interesante. Esperaba conservar una sólida estructura de peones que le permitiera aguantar hasta el final.
A pesar de que las blancas y las negras tienen 20 movimientos entre los que elegir el primero de la partida, solo se consideran buenos unos pocos de ellos. Estos son los primeros movimientos realizados en todas las partidas del torneo. La densidad refleja el número de veces que se realizó el movimiento.
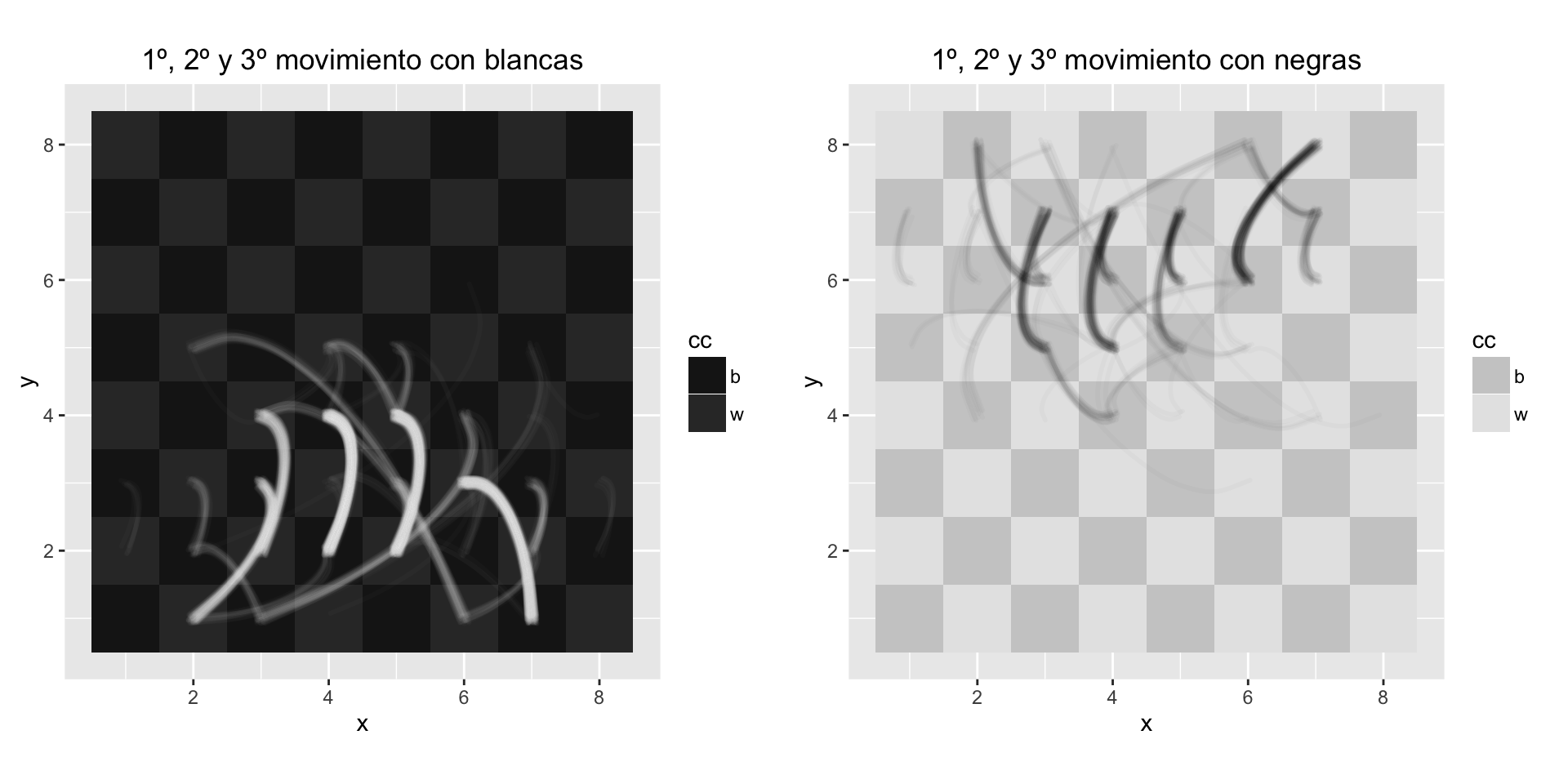
Para apreciar lo que sucede en un torneo de ajedrez en el que hay decenas de personas jugando simultáneamente, se puede usar este tablero en el que se van dibujando los primeros movimientos de todas las partidas simultáneamente. Es como ver superpuestas todas las partidas en un solo tablero, el pensamiento y la tensión de muchas personas reducido a unos segundos.
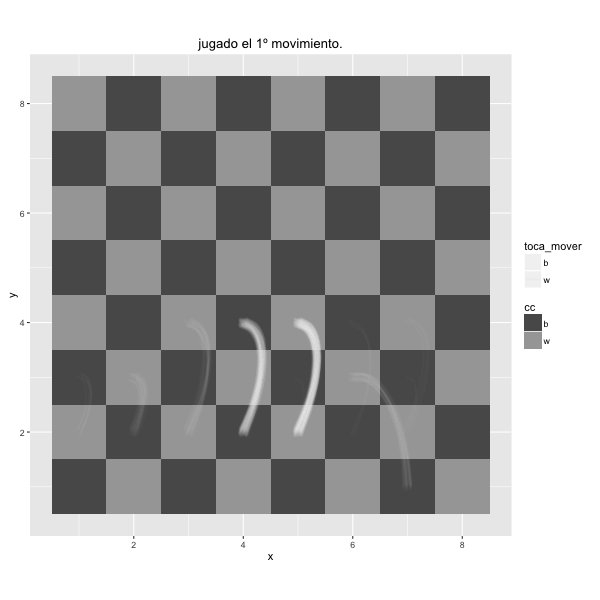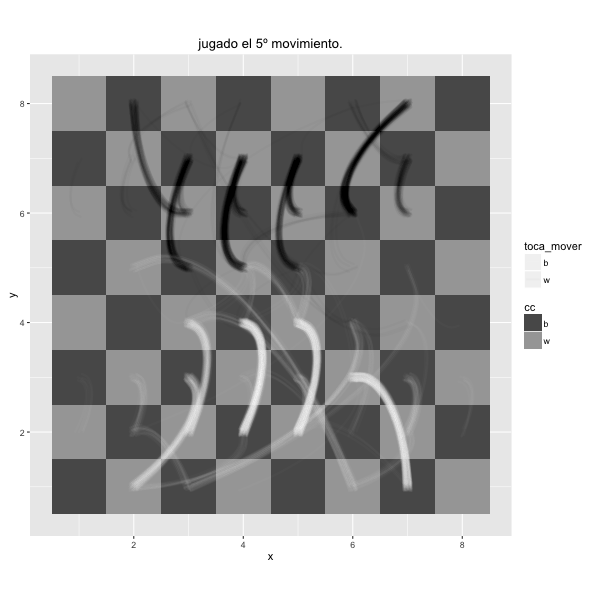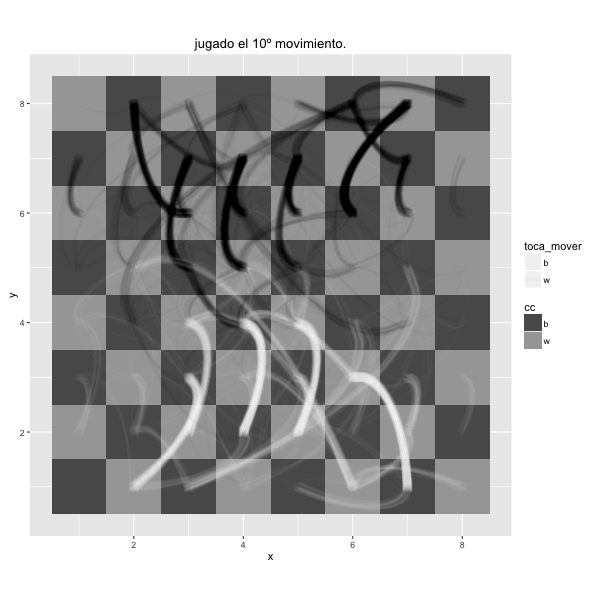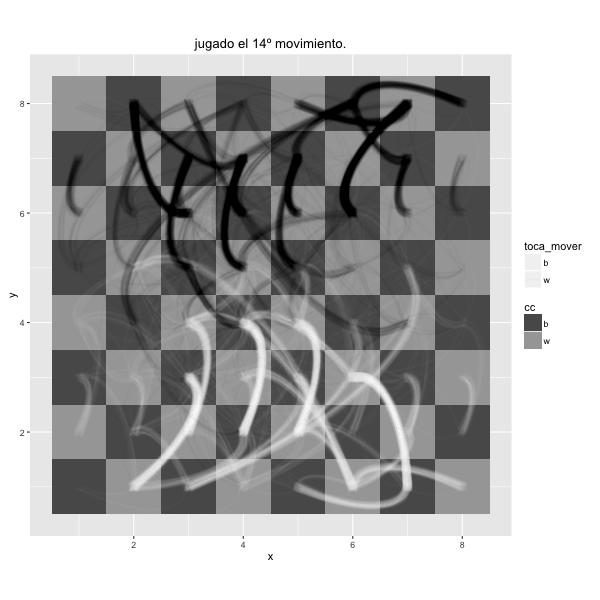
Mientras el otro pensaba, tuvo tiempo de observarlo. Tenia unos años más que él. No era la primera vez que lo veía, pero no conseguía ubicarlo. Se mordía las uñas y se tocaba la patilla, junto a la oreja, con la mano izquierda. Al cabo de unos cuantos movimientos, consiguió recordar. Iban a la misma academia de inglés, entraba cuando él terminaba, aunque nunca se habían saludado. A pesar de ello, sentía desprecio por él a causa de un comentario que le había escuchado hacía unos meses.
Los hechos habían sucedido de la forma siguiente: un día salía de su clase justo cuando entraban dos chicos mayores, chocaron con él fortuitamente al cruzarse en el pasillo, él había musitado “perdón” pero ellos no habían respondido, le habían mirado sorprendidos, como para dejarle claro que era casi invisible, y cuando se estaban yendo uno de ellos exclamó, entre risas, “¡pipiolo!”.
Realmente no sabía si el que había pronunciado la palabra había sido su rival o su amigo, pero poco importaba, ahora hasta tenía un motivo ético por el que vencerle. “¡Bien! Veamos quién es el pipiolo”, pensó mientras realizaba un movimiento. Sería estupendo ganarle y que el otro sintiera el dolor de su sofisticada venganza.
Juego medio
Los siguientes diagramas muestran la evolución media de todas las partida. La idea que deseo plasmar es la siguiente:
- En cada momento, un jugador puede elegir entre un conjunto reducido de movimientos legales.
- Este número de movimientos posibles, refleja hasta cierto punto los grados de libertad que tiene un jugador cuando elige la jugada. La intuición parecería indicar que quien tenga más libertad para elegir, tendrá más posibilidades de disponer de una jugada mejor.
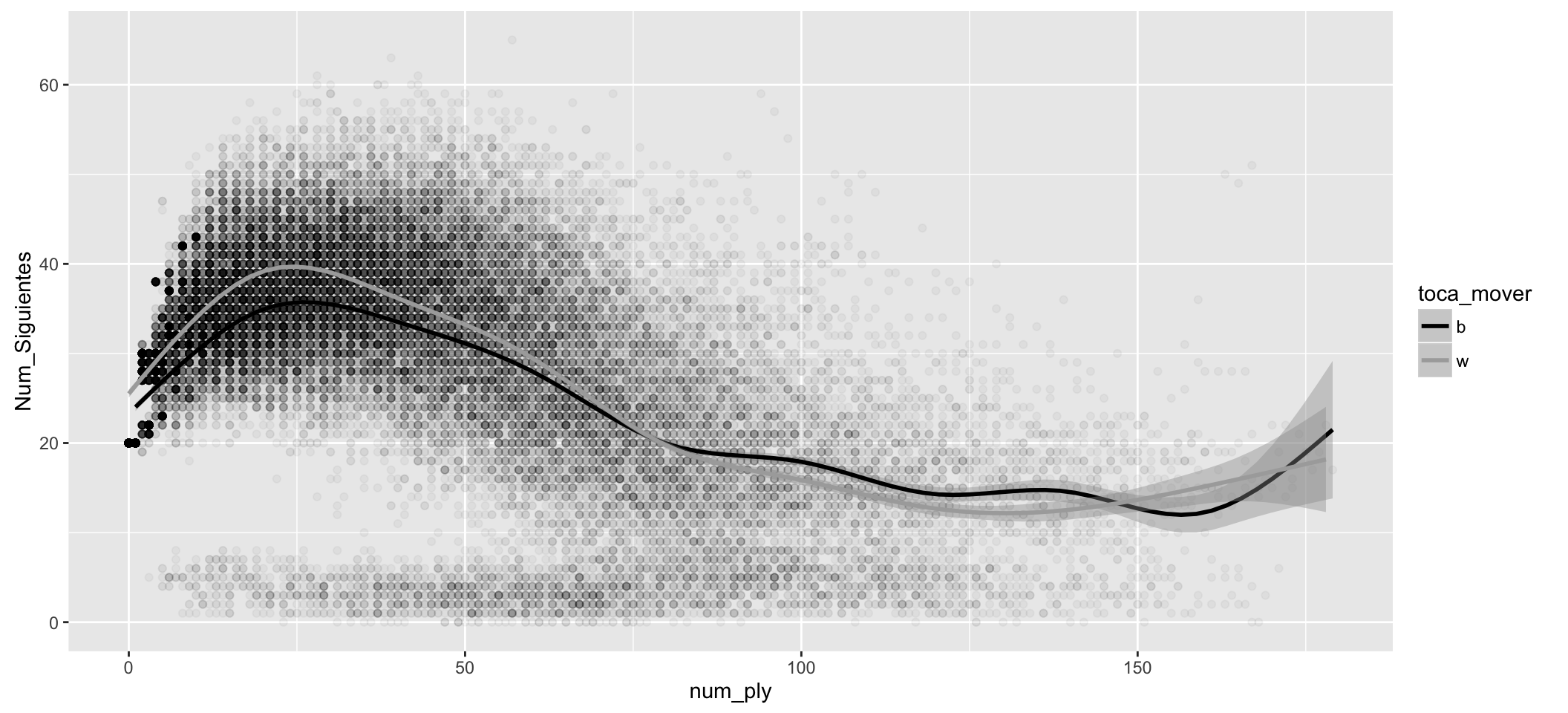
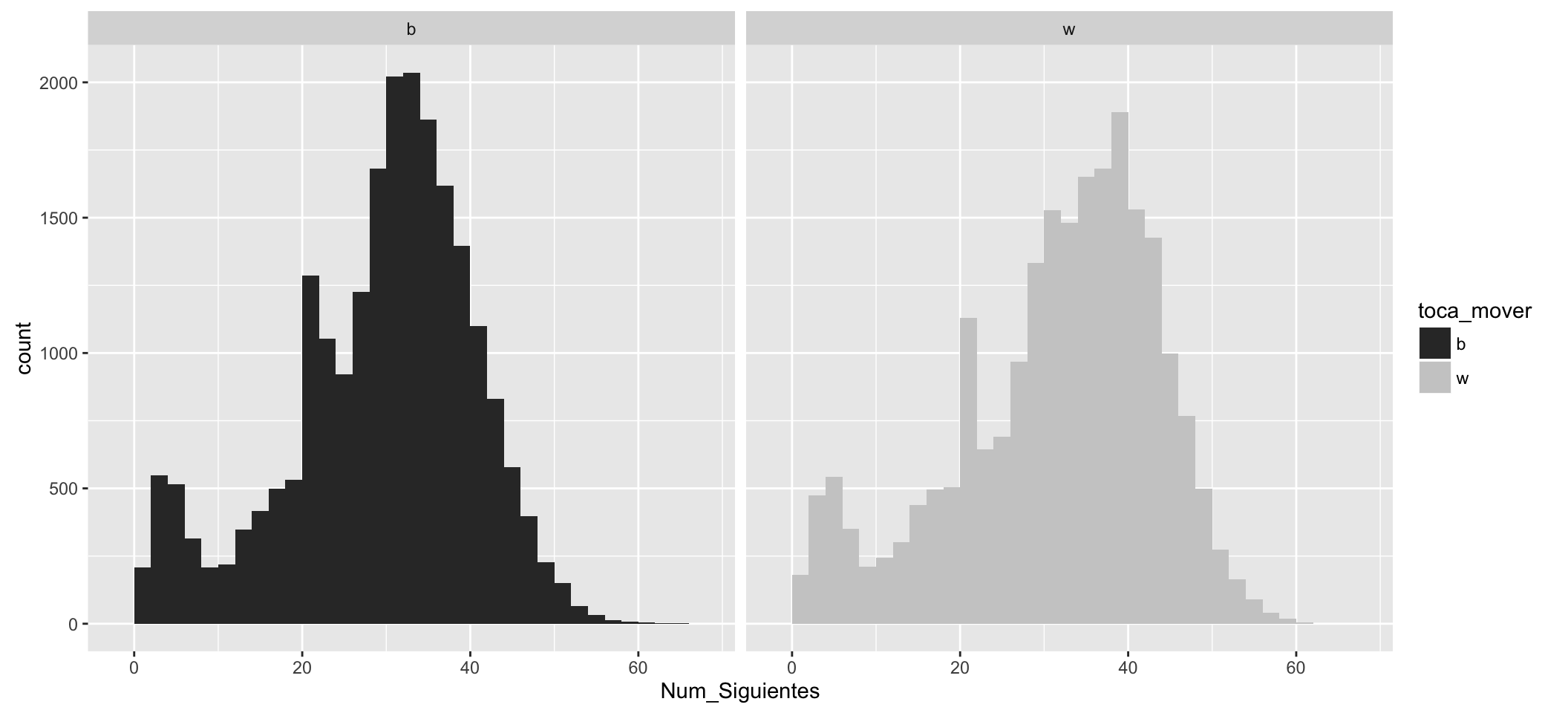
En los diagramas siguientes la nube de puntos refleja el número de movimientos posibles que tenían los jugadores en cada jugada. El primer diagrama refleja de forma combinada las blancas y las negras. Los dos siguientes reflejan la misma información de forma separada. Hay que tener en cuenta que las blancas juegan en los movimientos impares y las negras en los pares.
Separando los movimientos de las blancas y negras en sus respetivos diagramas:
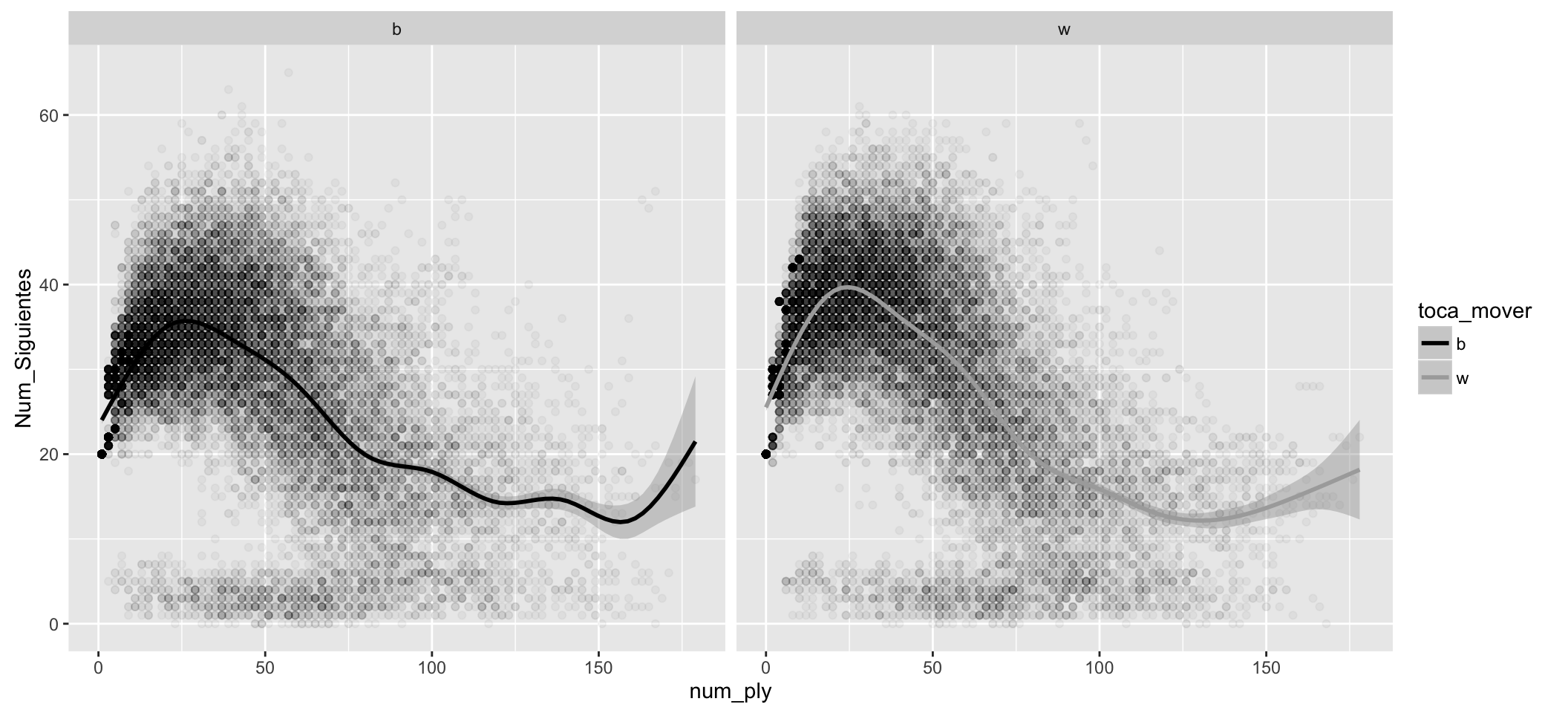
Los diagramas anteriores muestran varias cosas.
- Las blancas, de media, tienen más movimientos posibles al comienzo de la partida.
- Al comienzo de la partida los movimientos posibles son 20 en cada posición tanto para las blancas como para las negras (peones avanzando 1 ó 2 posiciones más los cuatro movimientos posibles de los caballos).
- El máximo de movimientos posibles (el máximo de la media es aprox. 40, para las blancas) se alcanza sobre los movimientos 25 a 30.
- Hay posiciones con más de 50 ó 60 movimientos posibles, sin embargo, son muy escasas.
- La nube de puntos se va haciendo más ligera conforme avanzan los movimientos. Es lógico, las partidas van terminando.
- A partir de la posición número 50 aprox. se comienzan a igualar los movimientos posibles, y, de media, bajan de 20 (son posiciones con pocas piezas en el tablero).
- Hay una nube de puntos más o menos uniforme a lo largo de todas las posiciones que está por debajo de 10 movimientos posibles. Esta nube corresponde a los jaques recibidos, que dejan pocas posibilidades para elegir a quien lo recibe.
Esto mismo, se puede apreciar en un diagrama en 3D en el que se sustituye la densidad de los puntos por la altura. En las solapas está la información de blancas y negras, si se conmuta, se aprecia que el diagrama de las blancas está ligeramente desplazado hacia el fondo al disponer de más movimientos siguientes en cada posición.
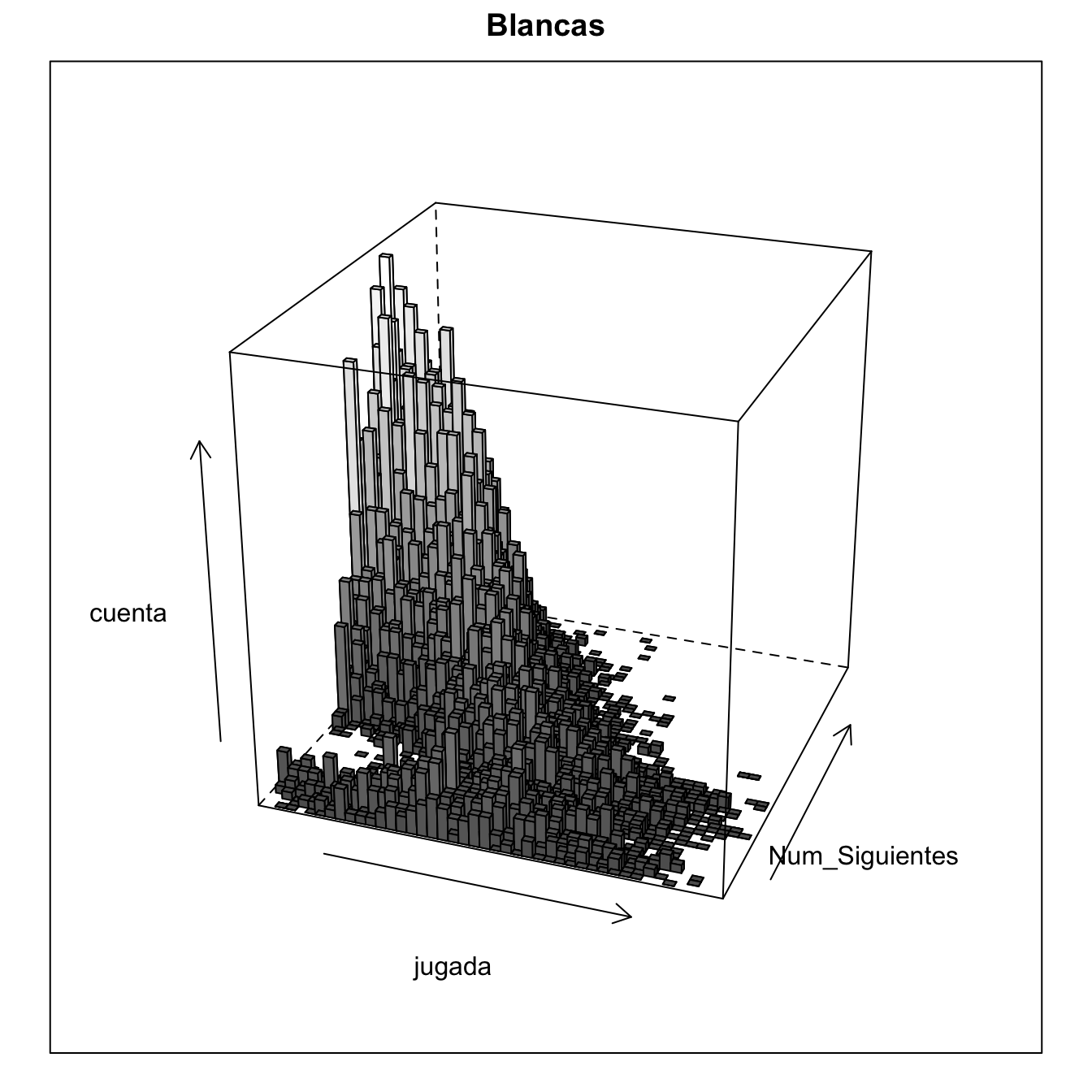
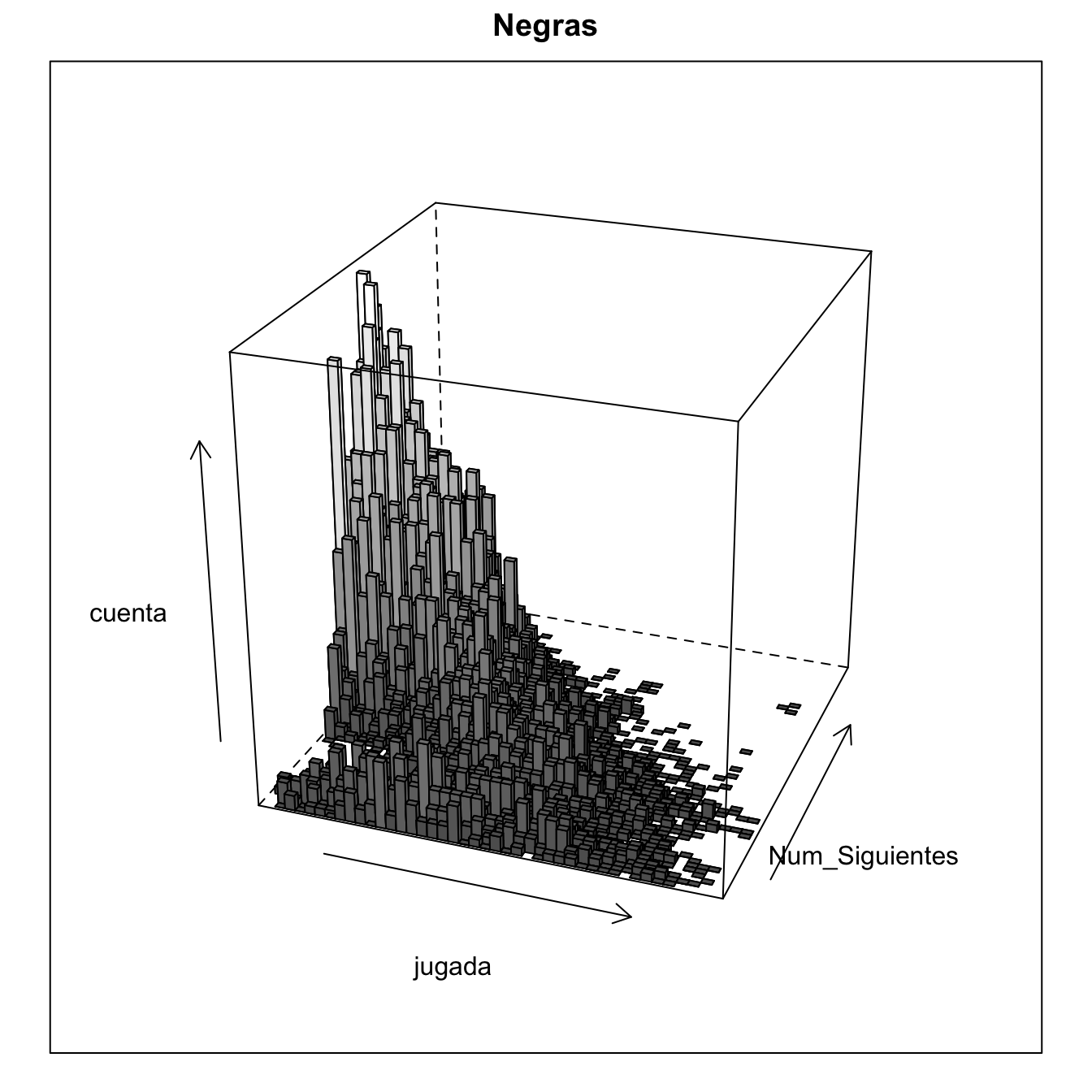
Número de posiciones en las que hay un número determinado de movimientos siguientes posibles.
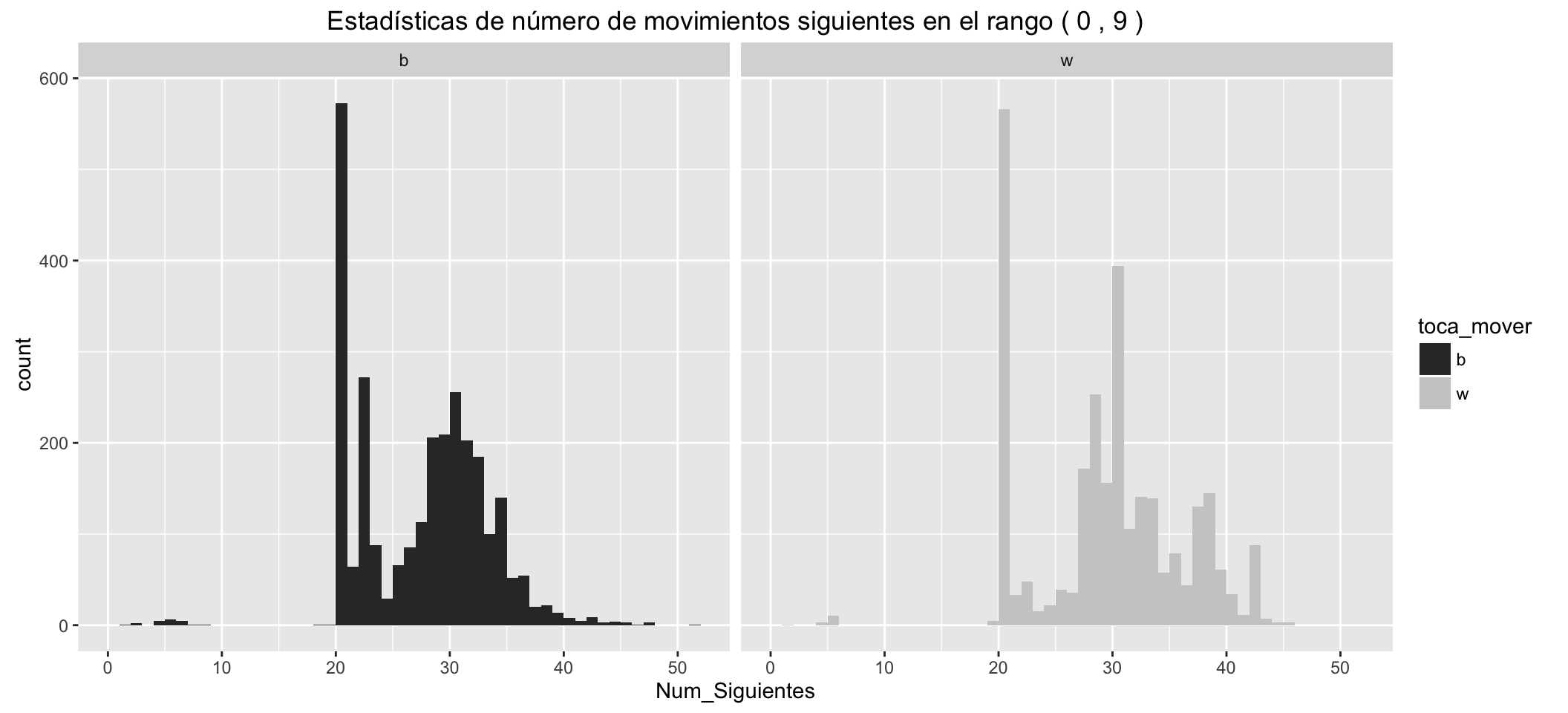
Quiero seguir profundizando en esta idea de los movimientos posibles para una posición dada. En las siguientes solapas he agrupado las posiciones en grupos de 10 y se muestra el corte de cada grupo en cuanto a movimientos posibles, mostrando, además, la información de la media, mediana, máximo, mínimo y quartiles.
 Movimientos siguientes posibles para las blancas:
Movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 24 | 33 | 31.02 | 40 | 61 |
Movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 22 | 31 | 28.92 | 36 | 65 |
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 24 | 30 | 29.11 | 33 | 45 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 22 | 28 | 26.97 | 31 | 51 |
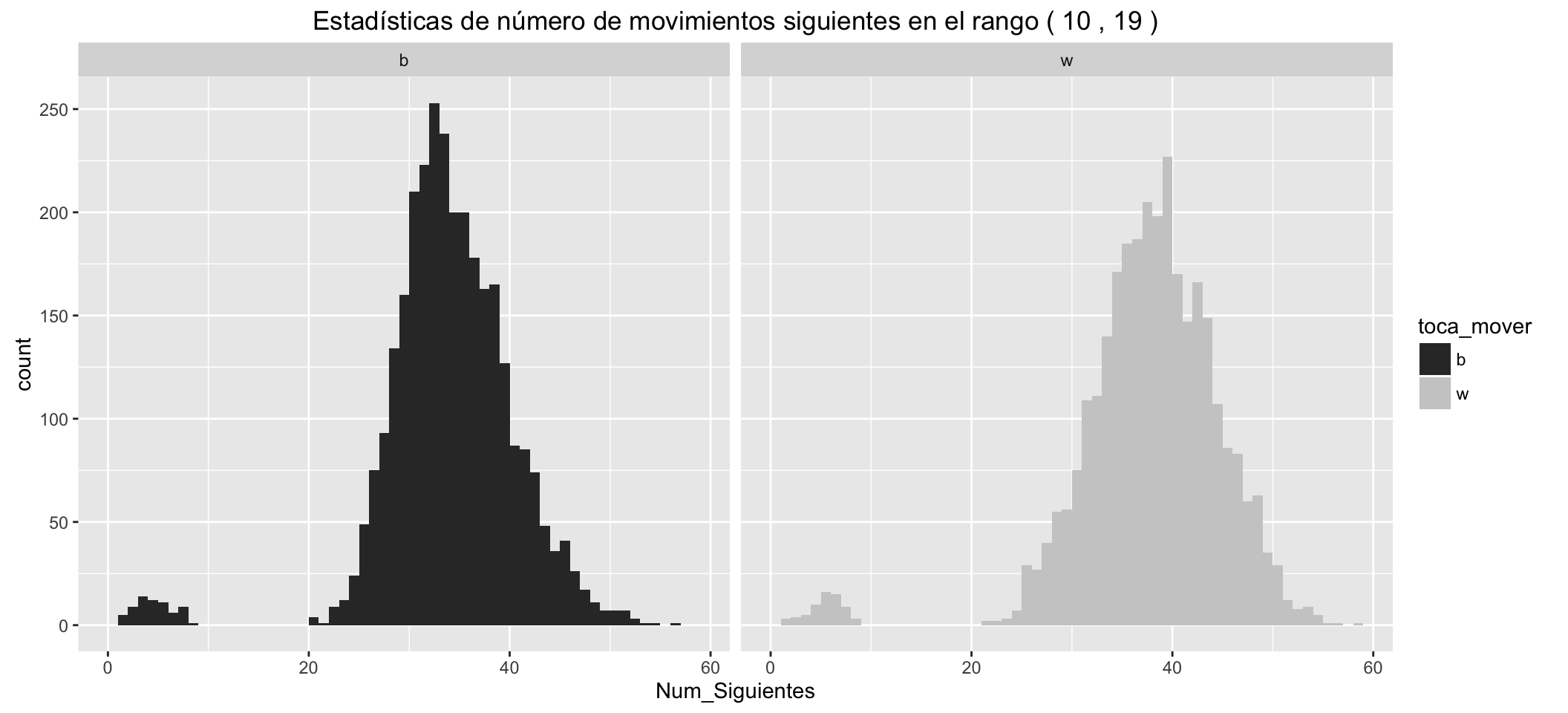
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 34 | 38 | 37.23 | 42 | 58 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 30 | 33 | 33.45 | 37 | 56 |
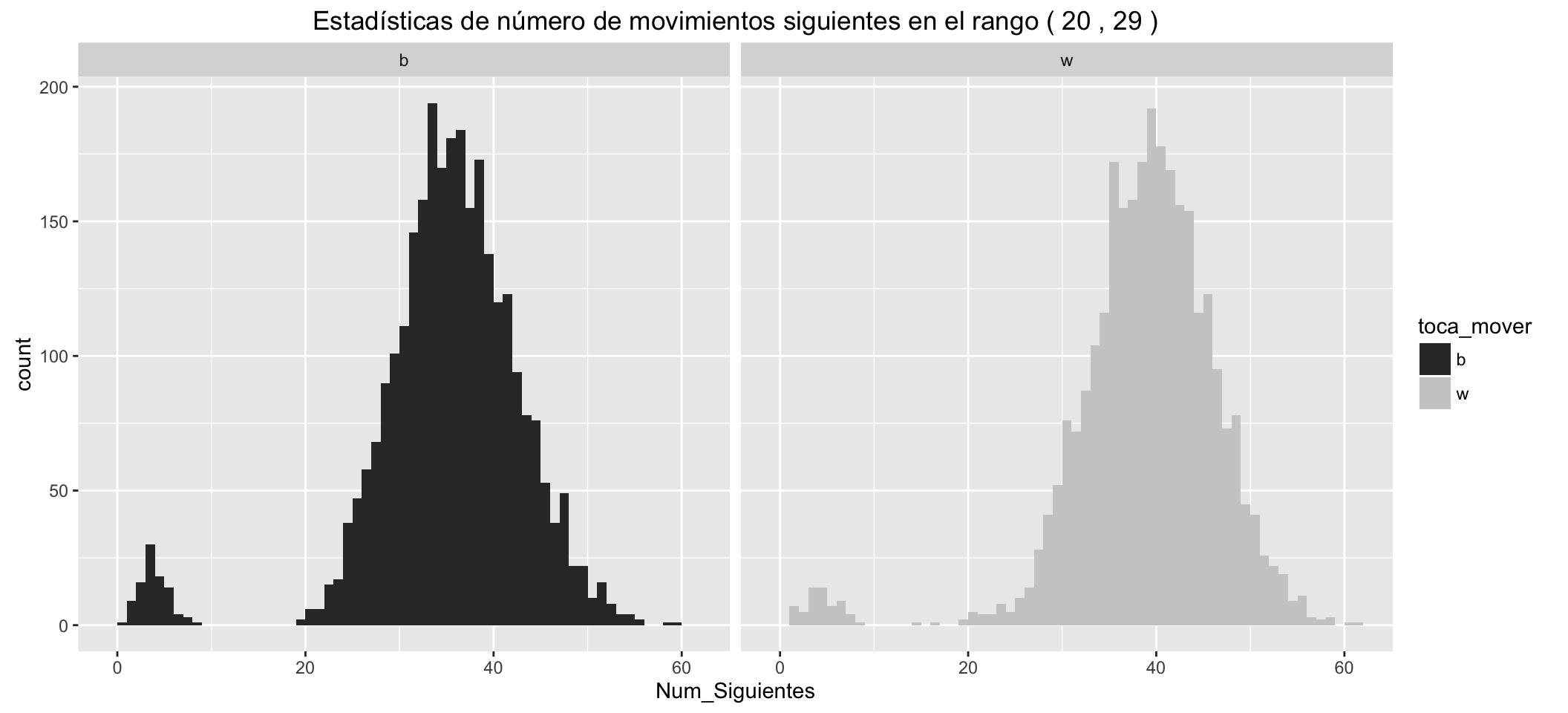
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 35 | 39 | 38.35 | 43 | 61 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 31 | 35 | 34.57 | 40 | 59 |
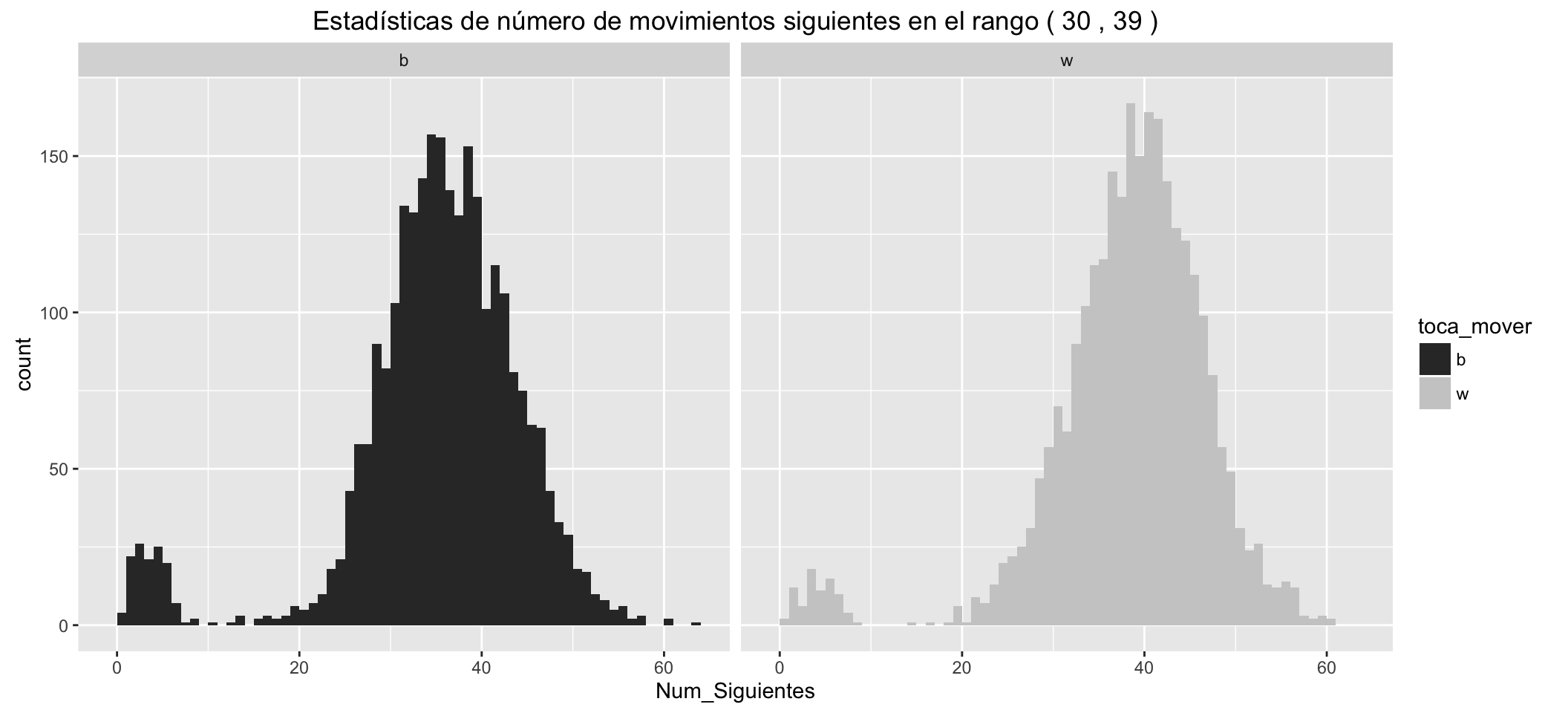
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 34 | 39 | 37.84 | 43 | 60 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 31 | 35 | 34.62 | 41 | 63 |
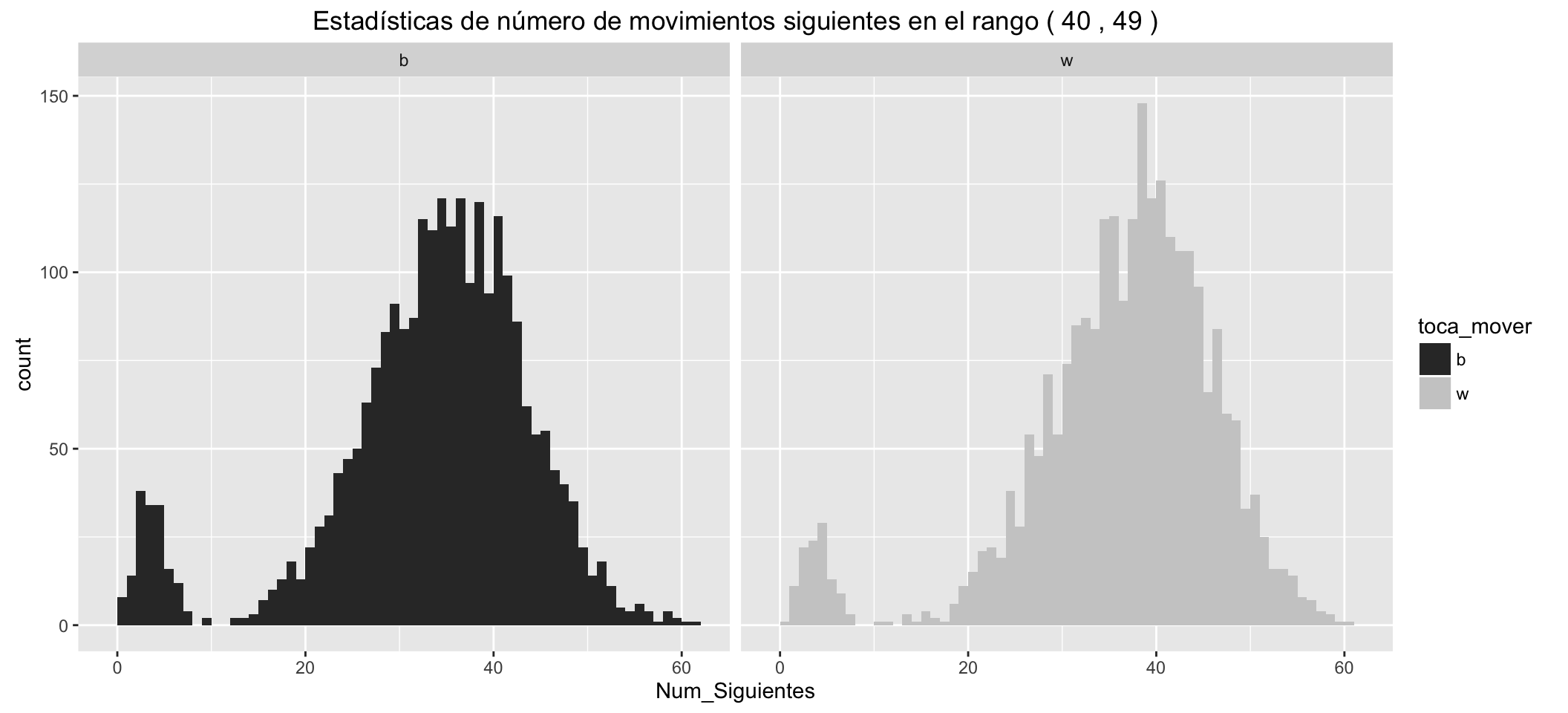
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 31 | 37 | 35.81 | 43 | 60 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 28 | 34 | 32.84 | 40 | 61 |
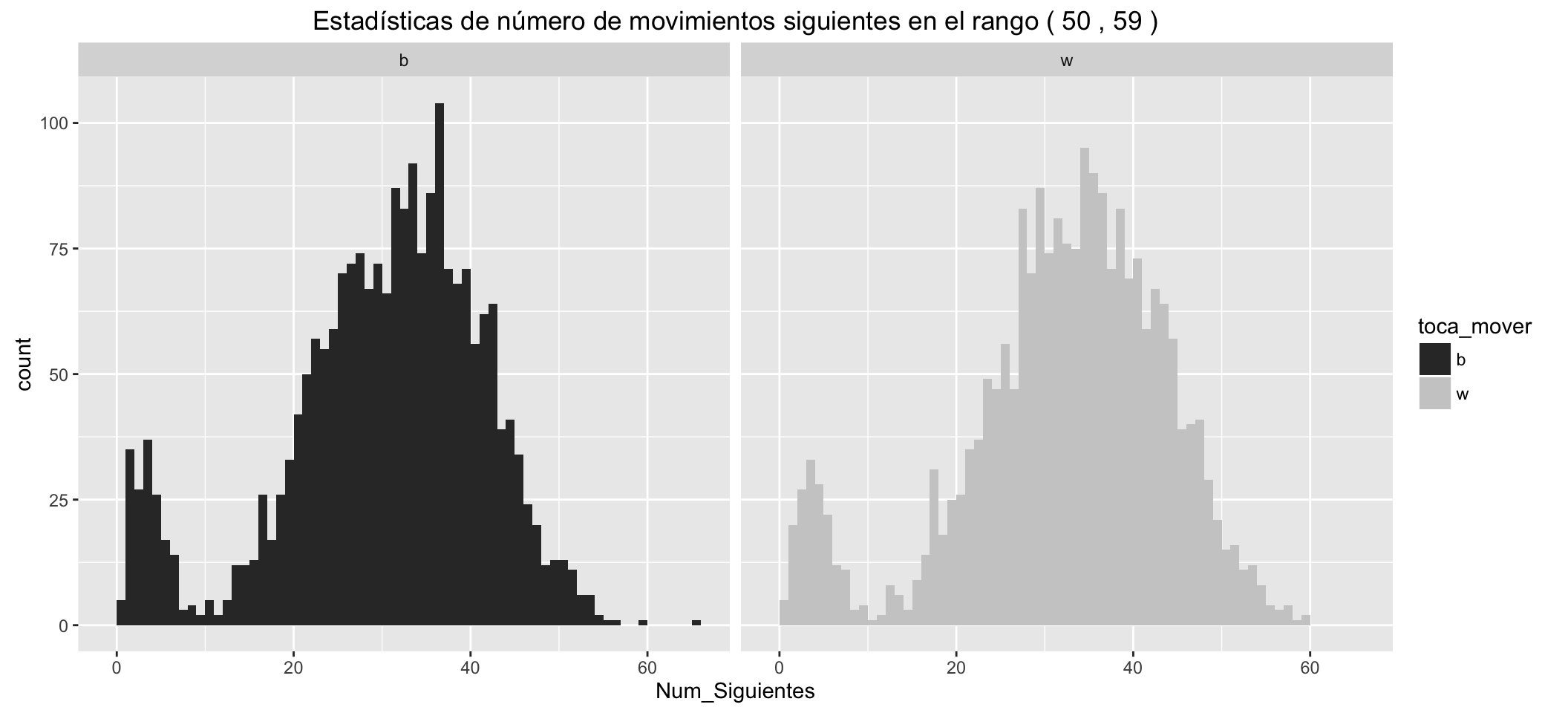
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 26 | 33 | 31.65 | 40 | 59 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 24 | 31 | 29.77 | 38 | 65 |
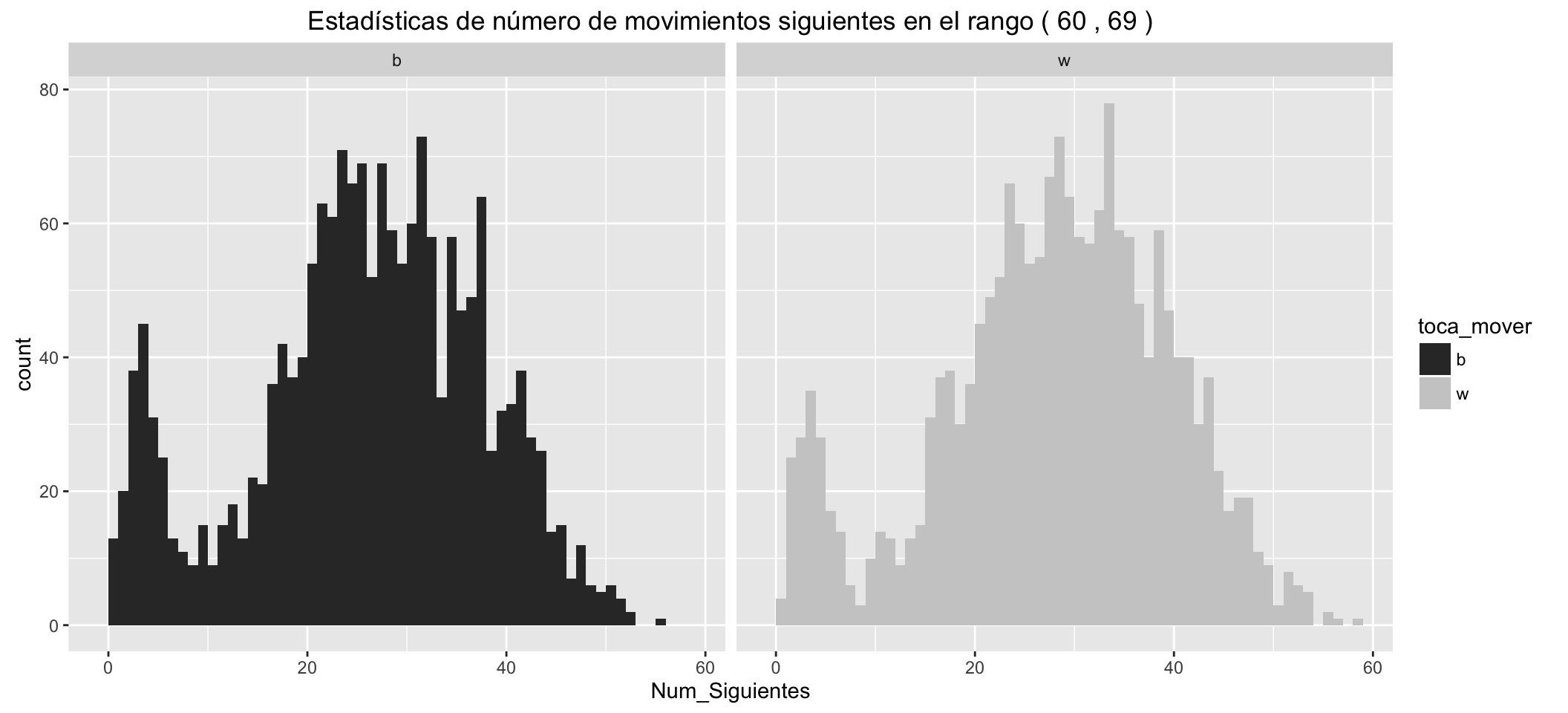
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 21 | 28 | 27.45 | 36 | 58 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 19 | 26 | 25.44 | 34 | 55 |
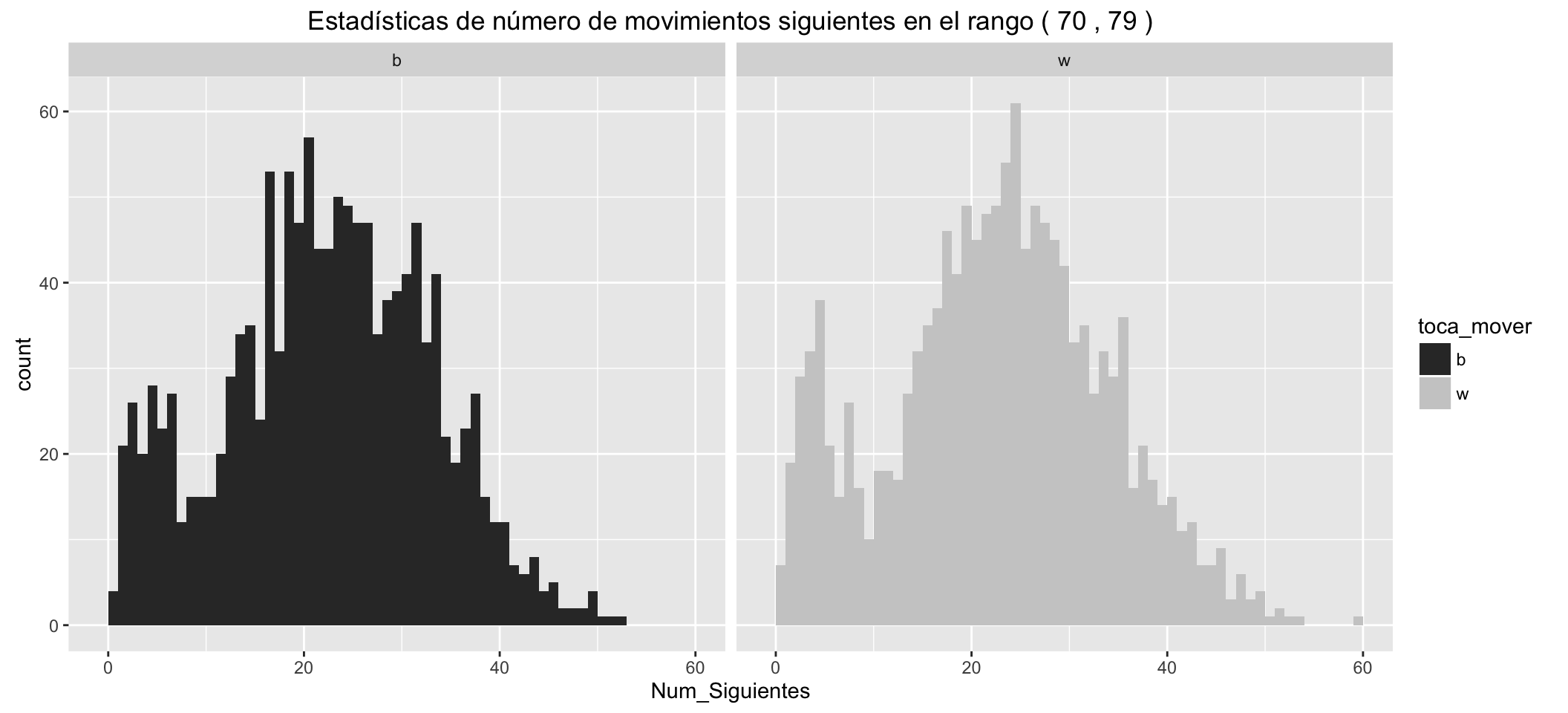
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 15 | 23 | 22.14 | 30 | 59 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 15 | 22 | 21.83 | 30 | 52 |
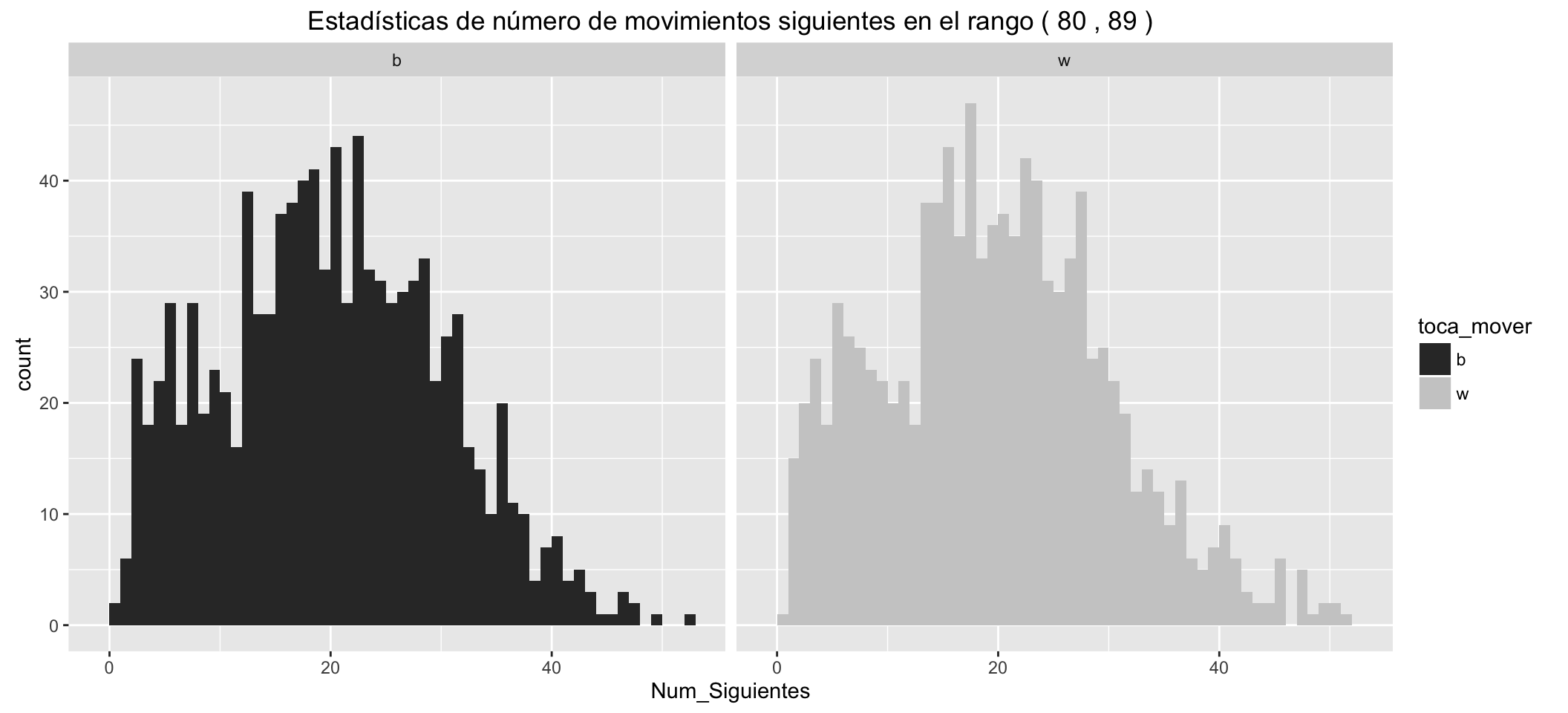
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 12 | 19 | 19.3 | 26 | 51 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 12 | 19 | 19.55 | 27 | 52 |
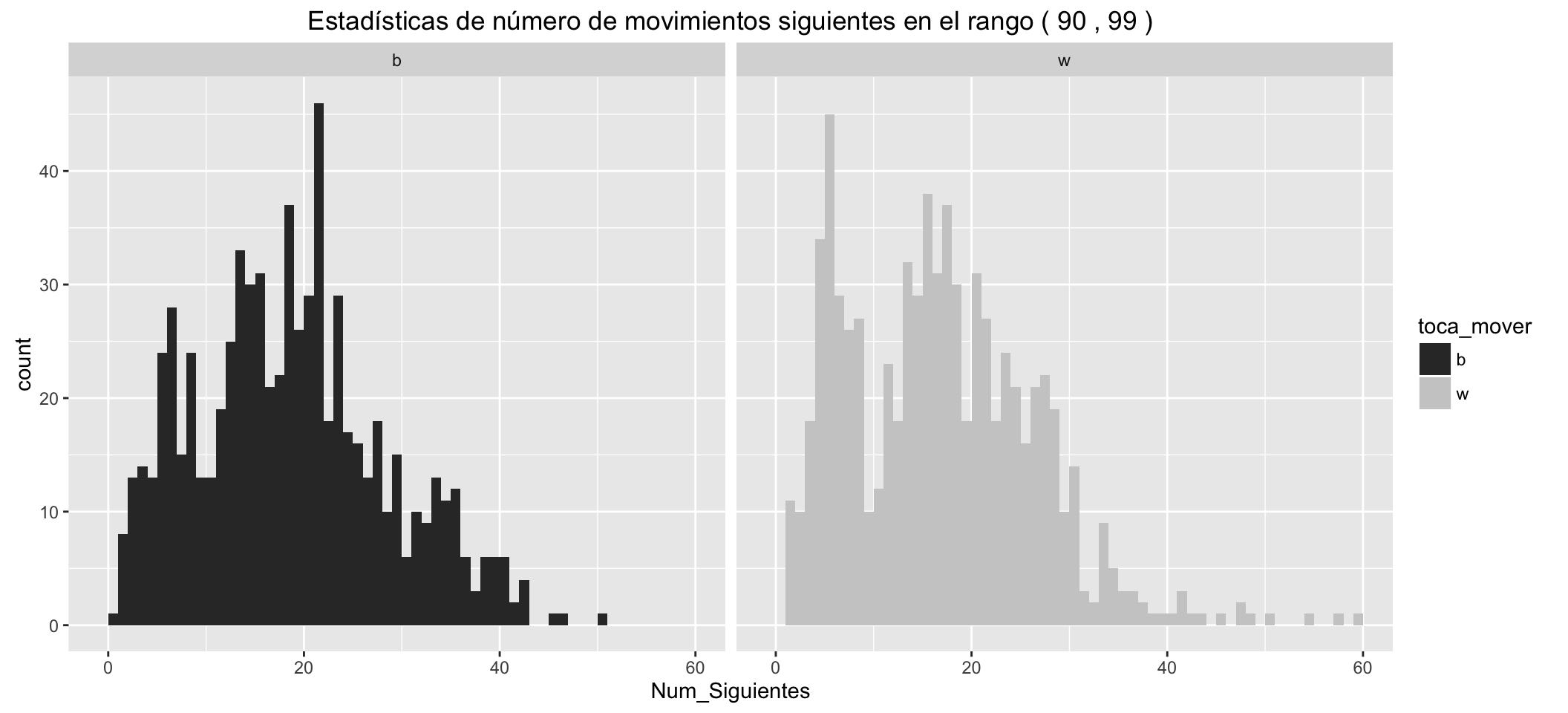
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 8 | 16 | 16.34 | 23 | 59 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 11 | 18 | 18.15 | 24 | 50 |
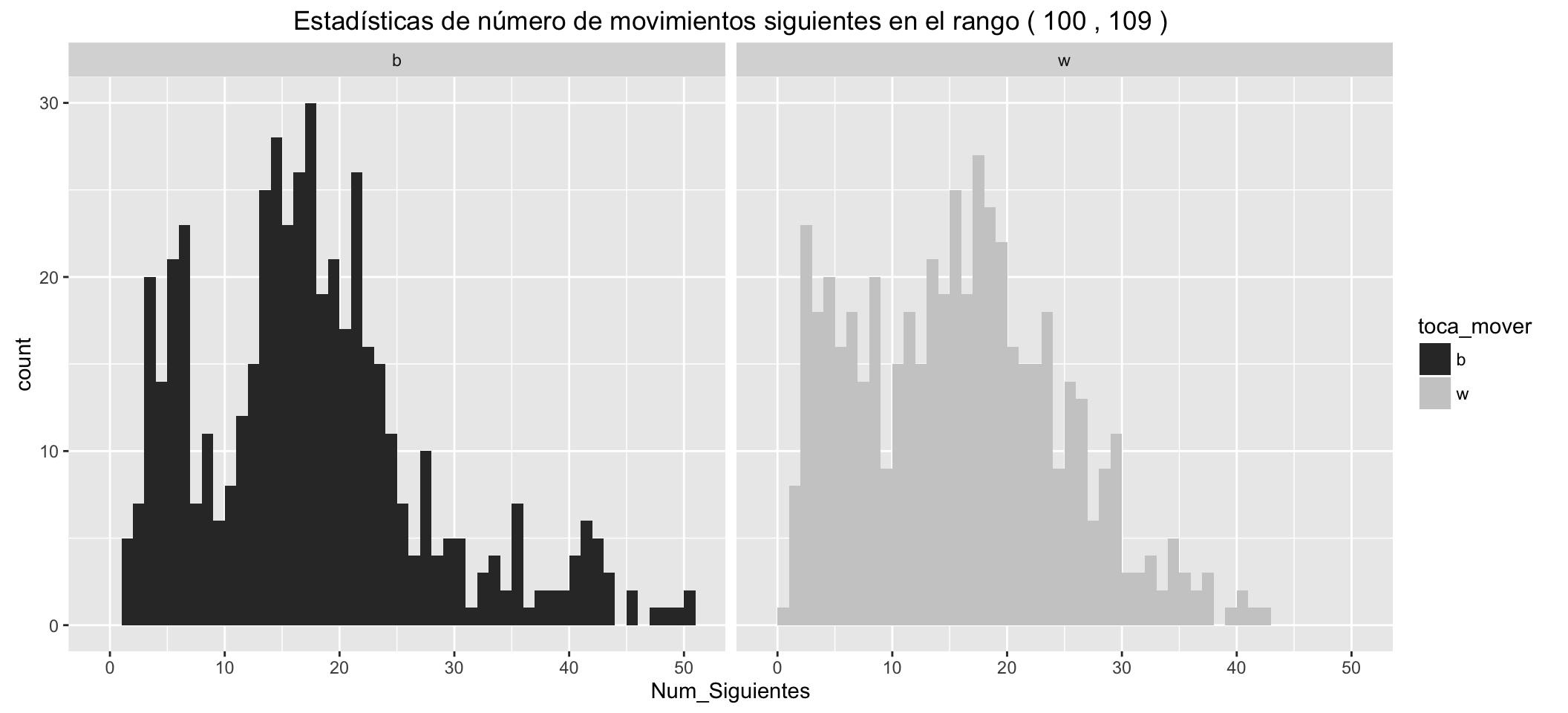
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 8 | 15 | 15.4 | 21 | 42 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 11 | 16 | 17.16 | 22 | 50 |
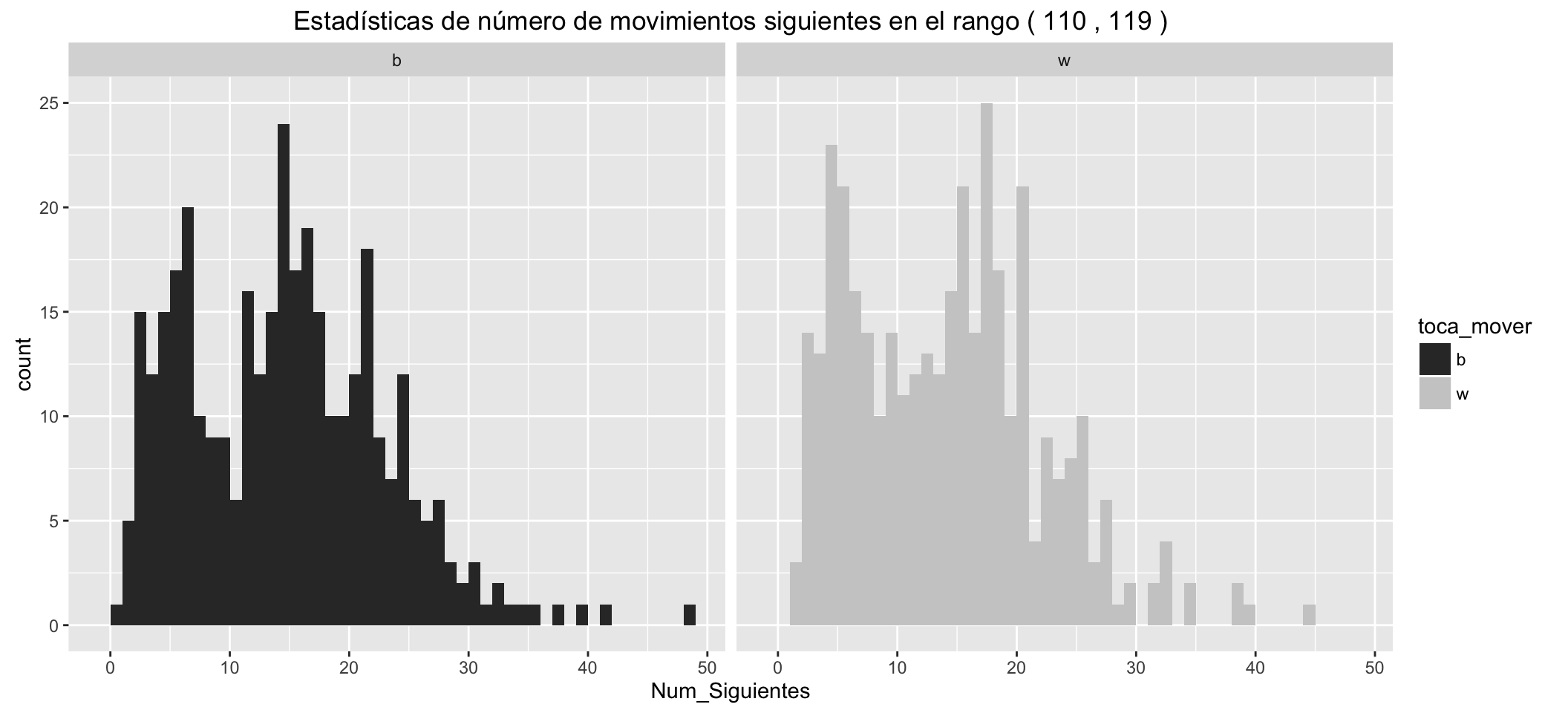
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 7 | 14 | 13.68 | 19 | 44 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 7 | 14 | 14.16 | 20 | 48 |
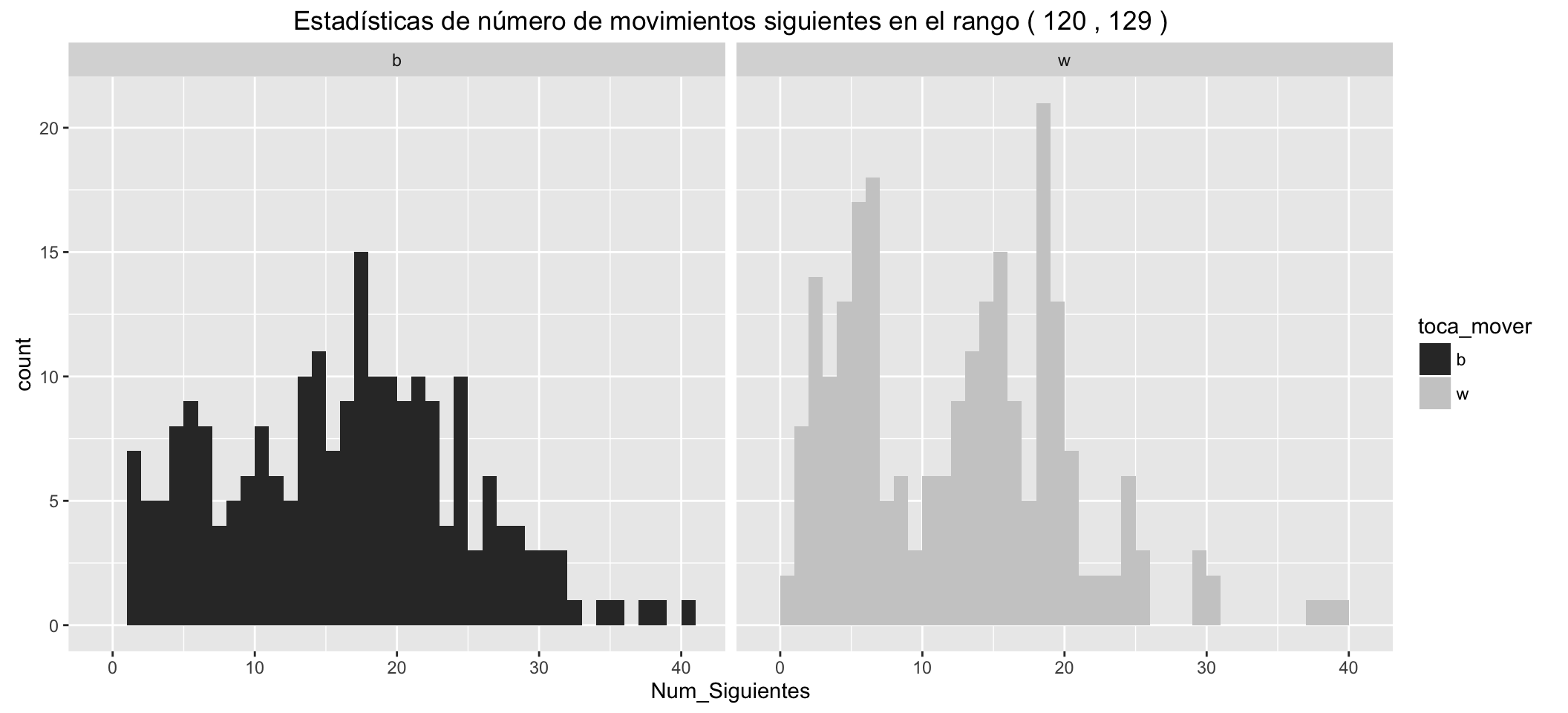
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 5 | 12.5 | 12.01 | 18 | 39 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 9 | 16 | 15.77 | 21 | 40 |
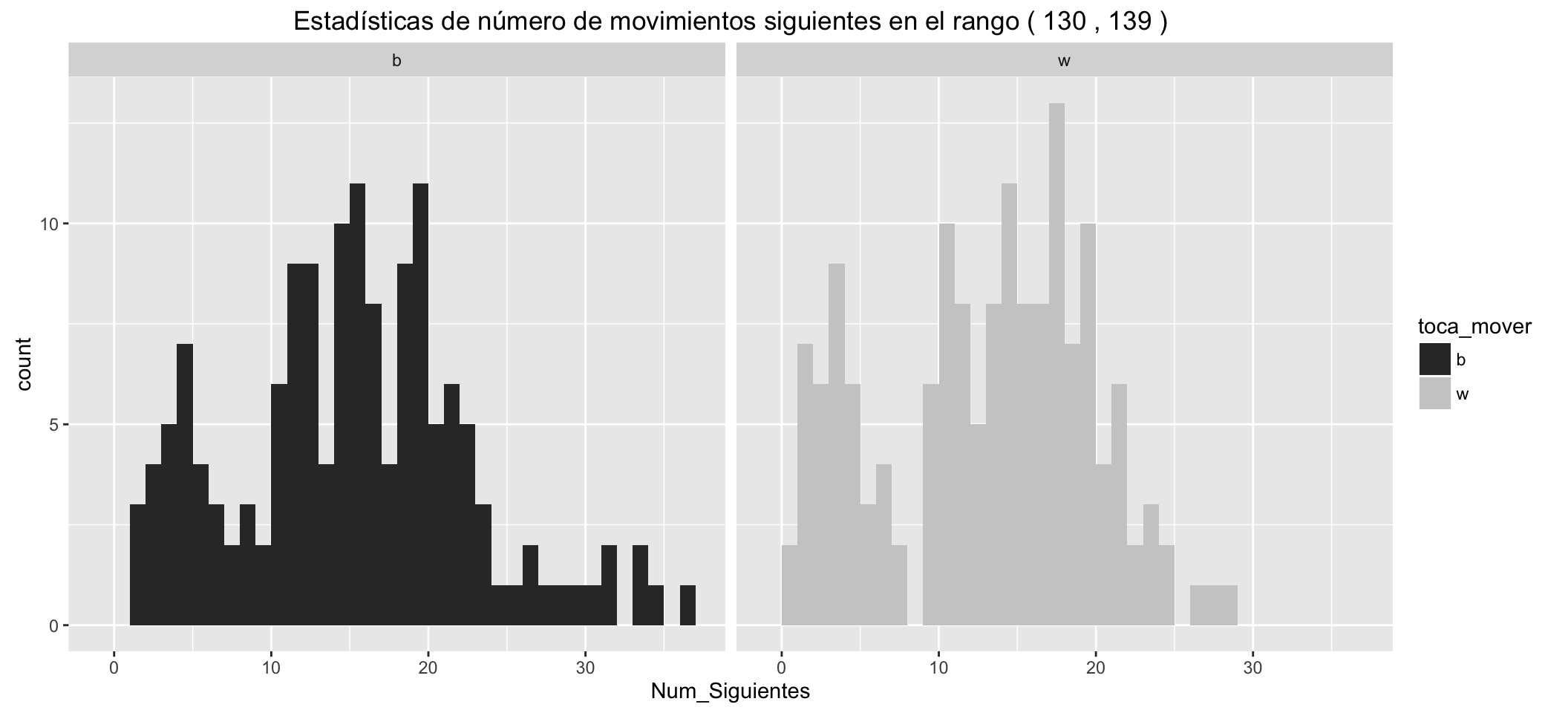
Estadísticas de número de movimientos siguientes posibles para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 7 | 14 | 12.52 | 17 | 28 |
Estadísticas de número de movimientos siguientes posibles para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 10 | 15 | 14.67 | 19 | 36 |
Se aprecian claramente:
- Los grupitos de movimientos en los que hay jaque, separados a la izquierda.
- Las blancas tienen, en los diferentes estadísticos, una ventaja respecto de las negras de unos cinco movimientos posibles más, en los primeros compases de la partida.
- Estas ventajas se reducen conforme avanzan los movimientos.
Miró el tablero y se resignó ante la cruda realidad, aún no estaba perdido. Para ser su primera partida oficial, con negras, contra un rival con elo… Bastante tenía con aguantar la posición. Llegar al movimiento cincuenta no estaba al alcance de todos.
Algunas mesas ya habían terminado, y sus jugadores se paseaban, en silencio, observando otras partidas. Estaban llegando al final, aún tenían las mismas piezas, los intercambios habían sido equitativos, había conseguido ver una celada, pero la iniciativa la mantenían las blancas. Durante un fugaz momento pensó en ofrecer tablas, ¡qué podía perder!, pero le dominó su orgullo, que aún esperaba ganar. Cayeron los dos últimos caballos, y los peones libres que quedaban. Entonces, fue su rival quien le ofreció tablas.
Final
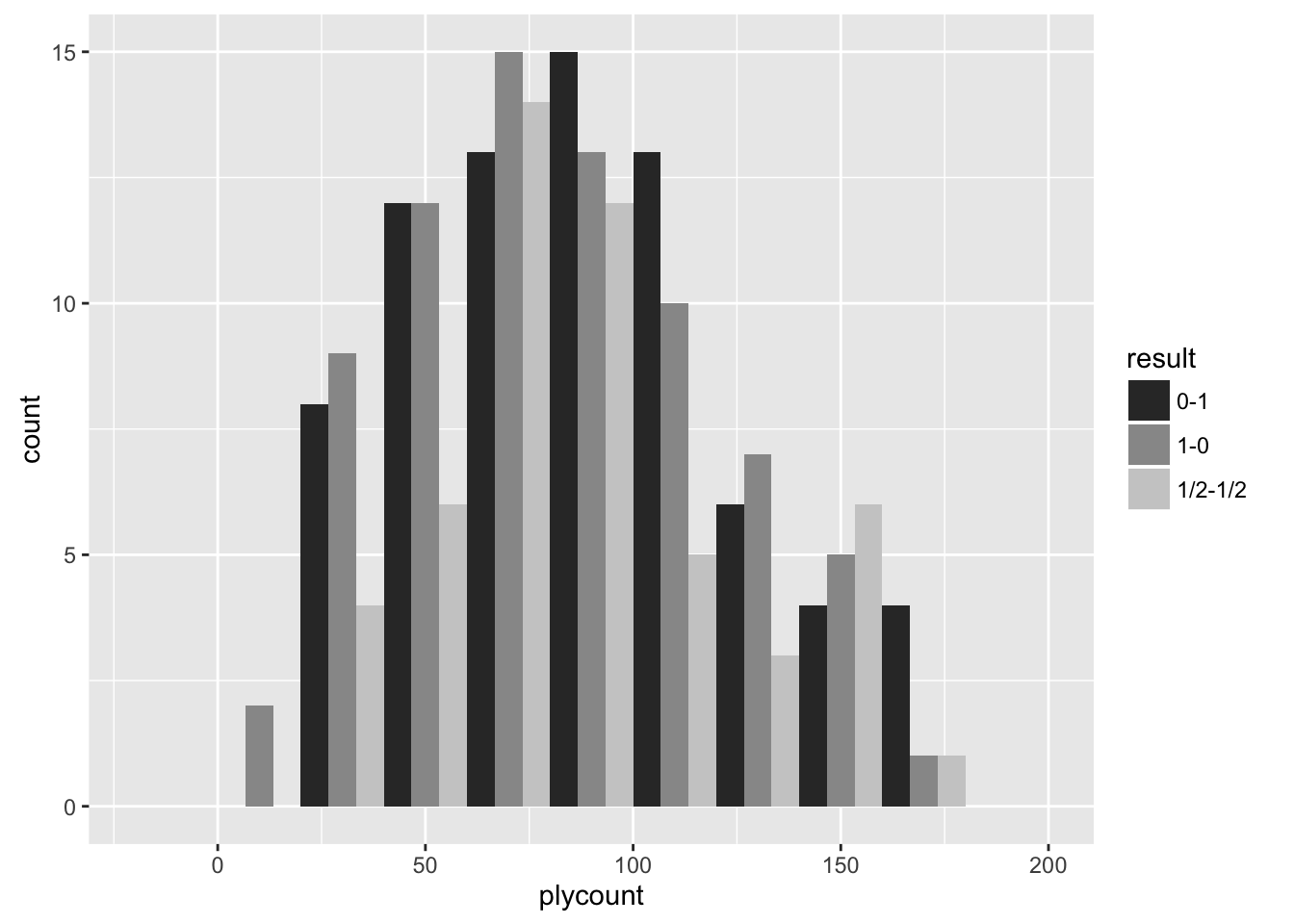
Las estadísticas al finalizar la partida, distinguiendo las blancas y las negras, son las siguientes en este torneo. Se muestra el número de partidas que terminana ganando en cada número de jugada. Las partidas que terminan hacia la derecha son las más largas (en número de movimientos).
Estadísticas del número de posición en que ganan las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | NA’s |
|---|---|---|---|---|---|---|
| 1 | 51 | 69 | 71.94 | 89 | 167 | 24 |
Estadísticas del número de posición en que ganan las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | NA’s |
|---|---|---|---|---|---|---|
| 23 | 58 | 72.5 | 79.36 | 97.25 | 168 | 25 |
Estadísticas del número de posición en que se producen tablas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. | NA’s |
|---|---|---|---|---|---|---|
| 20 | 67 | 80.5 | 86.47 | 102.8 | 173 | 10 |
De los datos se observa que, proporcionalmente, las blancas ganan más en las partidas más cortas, las negras necesitan más movimientos para ganar, y para las tablas se requiere aún más. Al menos en este torneo.
¿Está relacionado de algún modo con el número de movimientos siguientes posibles? Si vemos los datos estadísticos de las victorias de las blancas frente a las negras y viceversa:
Movimientos siguientes posibles en partidas que ganan las blancas
Para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 27 | 35 | 33.33 | 41 | 61 |
Para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 21 | 30 | 27.51 | 36 | 58 |
Movimientos siguientes posibles en partidas que ganan las negras
Para las blancas:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 0 | 21 | 31 | 28.95 | 38 | 60 |
Para las negras:
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1 | 25 | 32 | 30.58 | 38 | 65 |
Sin entrar en un análisis estadístico formal, parece que, de media, cuando ganan las blancas, estas tienen 5 movimientos posibles más entre los que elegir.
Por el contrario, en las partidas que ganan las negras, estas tienen, de media, 1,5 movimientos más entre los que elegir, y hay que tener en cuenta que, respecto de los primeros movimientos, las negras han tenido que compensar una desventaja de unos 5 movimientos posibles.
Luego, los datos parecen corroborar que, hasta cierto punto, la victoria en las partidas, guarda relación con el número de movimientos posibles en cada movimiento. Podríamos estudiar la correlación y establecer un modelo para predecir la victoria de uno u otro a lo largo de la partida, pero eso tendrá que ser en otro artículo.
Epílogo
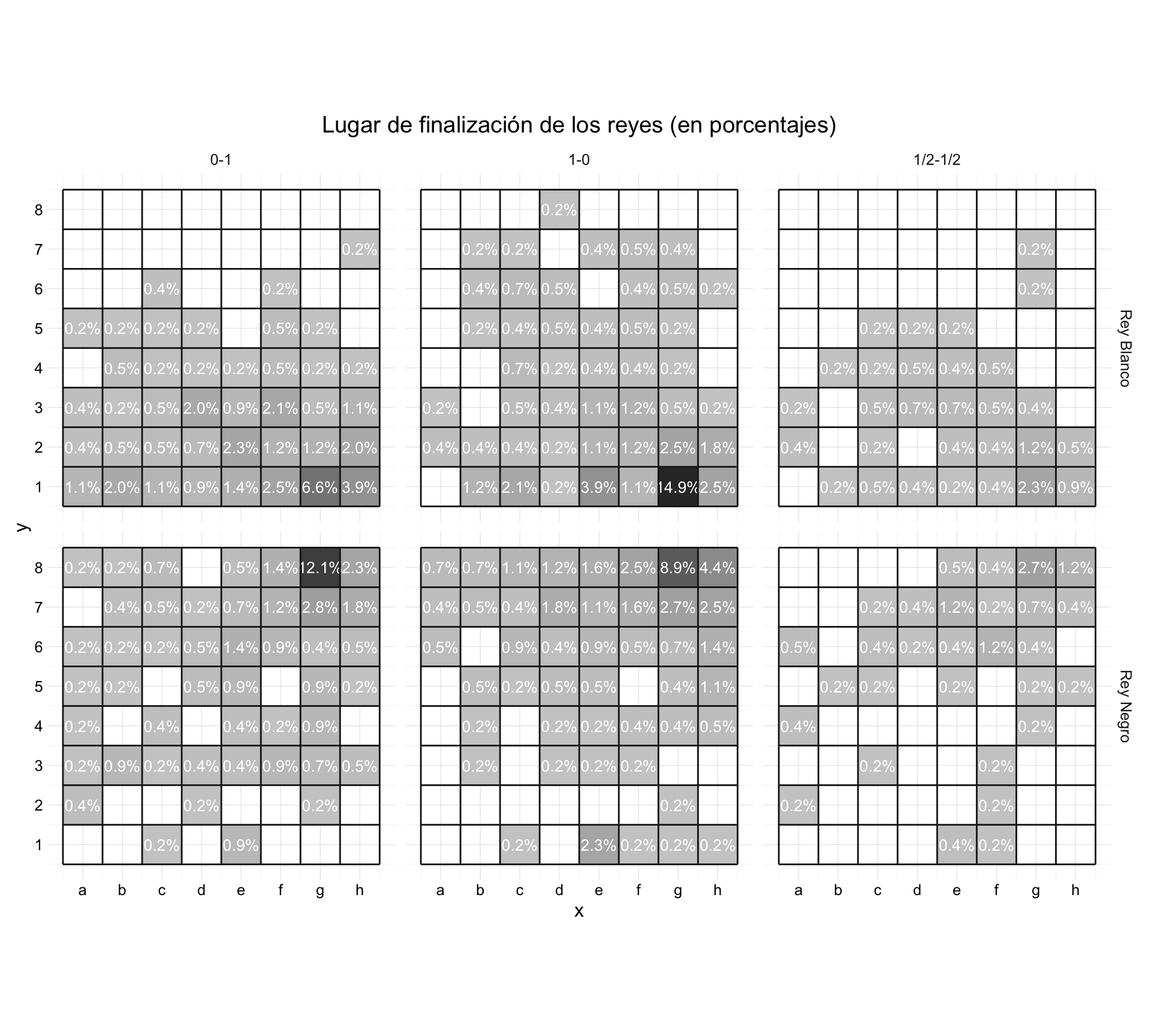
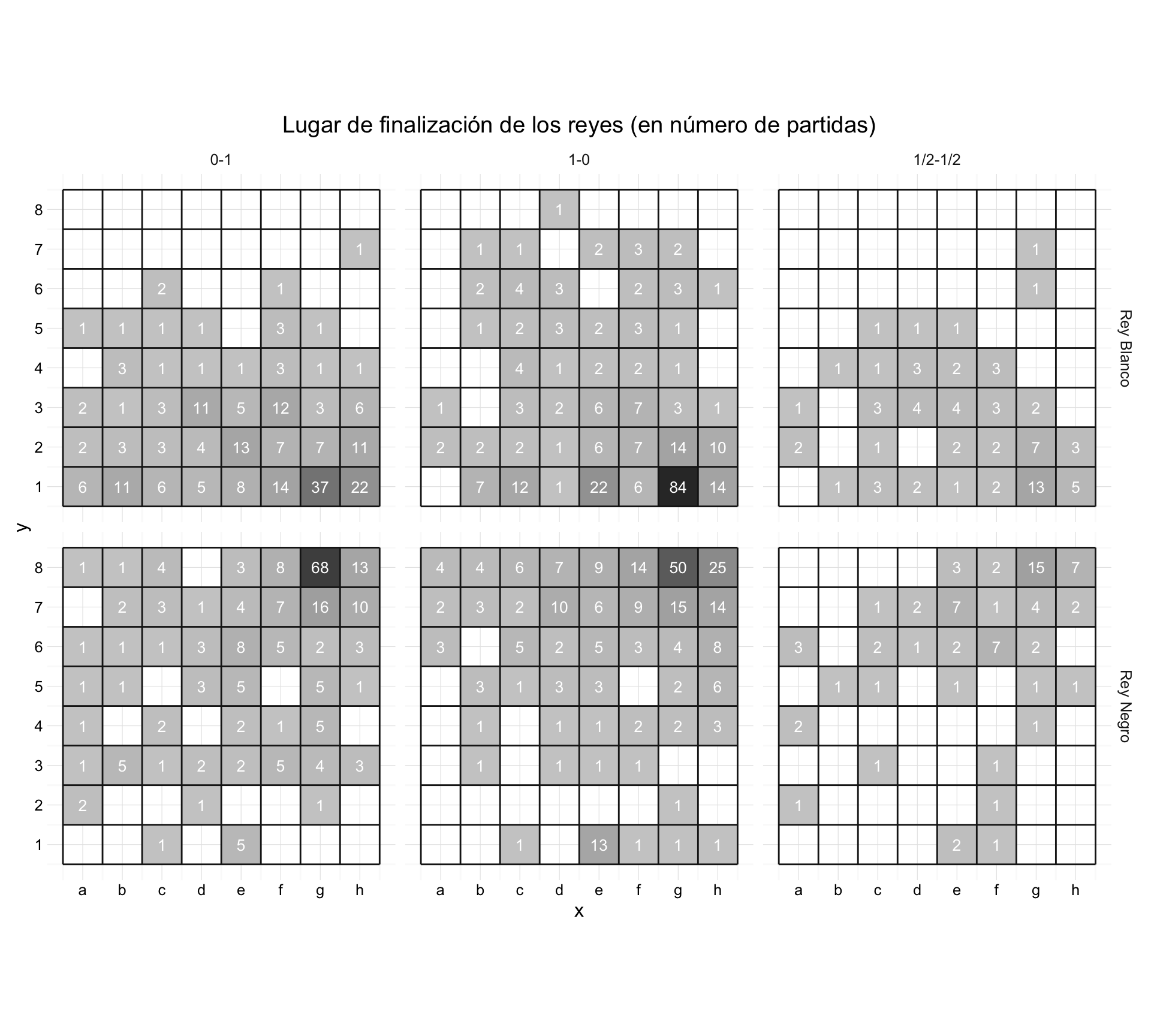
Una última pincelada, cuando la partida acaba ¿dónde está el rey?, en los siguientes diagramas se muestran las posiciones que reflejan claramente el enroque de los reyes. Parece que, tanto en número de partidas, como en porcentajes, el enroque mejora las probabilidades de victoria.
Lugar de finalización de los reyes
El otro no mostraba ningún signo de recordarle de nada. Venció a su orgullo y aceptó. “¿Hace mucho que juegas?”, preguntó su oponente. “Es mi primera partida oficial”, respondió. “¡Enhorabuena! Has jugado muy bien”. Sonrió, la ofensa del pasado se le borró del pensamiento. Lo miró y respondió sinceramente “Gracias”, y añadió, “tú también”.
Fin
Enlaces de interés
Para más información sobre el concepto de movilidad en el ajedrez, ver: Chess Programming Wiki / Mobility
Agradecimientos
Quiero expresar mi agradecimiento a Joshua Kunst por su paquete para R rchess y las ideas del código, en algunos diagramas, que he tomado prestado.